
Bill Tankersley's EMT 668 Page
Write-up 10
Polar Equations
In this write-up, we will concentrate on investigating the following
polar equations and their graphs:
1. 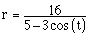 , 2.
, 2. 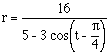 , and 3.
, and 3. 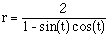
Looking at the graph of equation 1 above, we get something like the following:
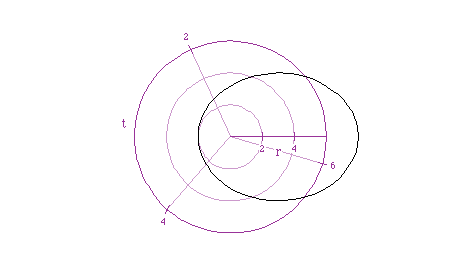
Let's look at another equation of the same form, such as 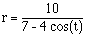 . Here is the
graph of this equation:
. Here is the
graph of this equation:
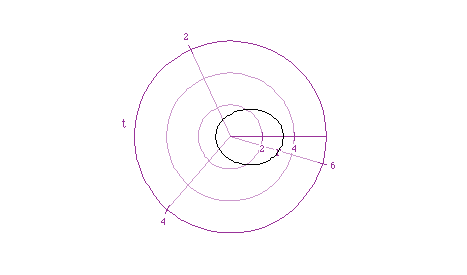
After experimenting around with other graphs of this type equation,
we noticed that different numbers a, b, and c have a different effects on
the graph of equations of the type 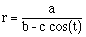 .
.
What we see here in both cases is that we get an ellipse whose major axis
is the r axis and whose minor axis is the t axis.
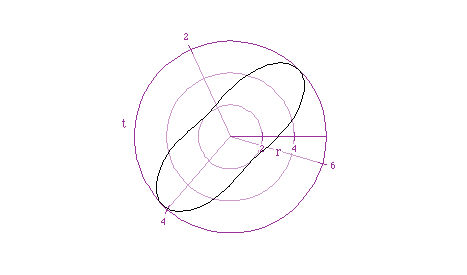
Looking at the graph of equation 2 above, we get this:
Again, we get an ellipse, but it looks like the major axis is along
the angle for pi/4, or 45 degrees. This must surely be related to the pi/4
in the polar equation above. Let's look at another example of a graph of
this type, say 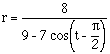 . Here is the graph:
. Here is the graph:
Notice that the major axis of the ellipse is the line Pi/2, or 90 degrees.
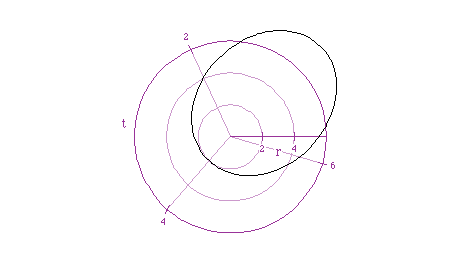
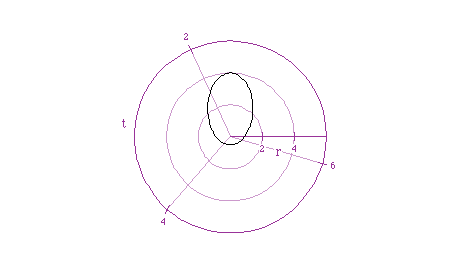
So, we can definitely say that the angle controls the orientation of the
ellipse. Also, the values of a,b, and c control the size of the ellipse
for graphs of the form 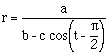 .
.
Next, for the graph of equation 3 above, we get the following:
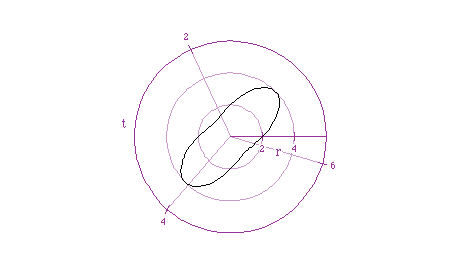
Let's look at a graph of another function of the same type, say 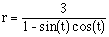 .
Here is the graph:
.
Here is the graph:
Clearly, changing the value in the numerator from 2 to 3 has lengthened
the major axis of the figure above. One can make some very interesting graphs
by multiplying t by various values in this form also.
This concludes the investigation of polar graphs of the given forms for
this particular problem. Polar graphs have always been interesting to me,
and it is nice to have a program such as Theorist with which to explore
various graphs.
Return to Bill Tankersley's EMT 668 Page


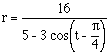 , and 3.
, and 3. 


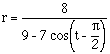 . Here is the graph:
. Here is the graph:
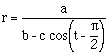 .
.
