

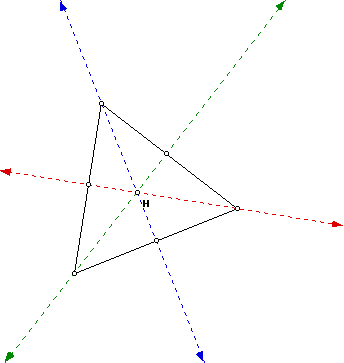

In the second triangle above, notice that the angle at the bottom
left of the triangle is close to being a right angle. Also, notice that
the orthocenter is fairly close to that angle. After experimenting with
several triangles of the same shape, I began to wonder about the location
of the orthocenter on right triangles.
Below, we see two right triangles and their orthocenters:
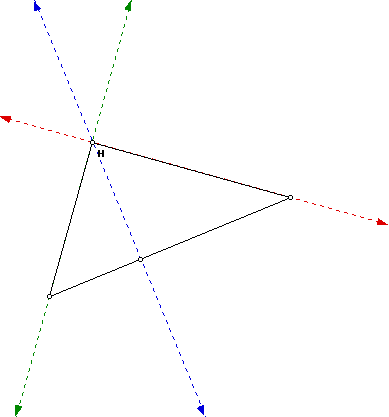
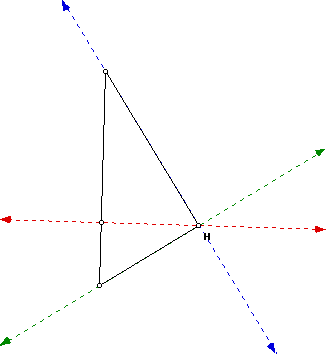
After observing many right triangles and the location of their orthocenters,
I feel safe in claiming that the orthocenter of a right triangle will always
coincide with the vertex of the right angle.
Now, we are interested in looking at some obtuse triangles and the locations
of their orthocenters. Since the orthocenters in right triangles moved to
a vertex, I began to wonder if the orthocenters in obtuse triangles would
be located at some point outside the triangle.
Here are two obtuse triangles with their orthocenters:
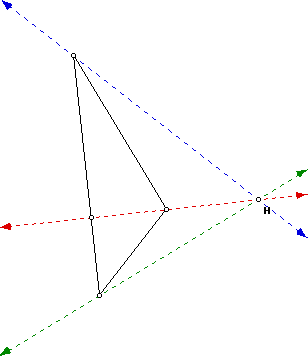
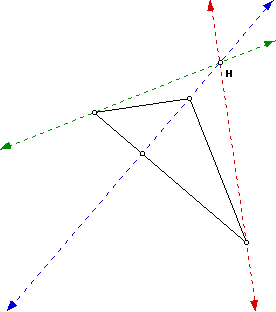
After observing several examples of obtuse triangles, I feel confident
in making the statement that the orthocenter of an obtuse triangle lies
on the extension of the altitude to the side of the triangle that is opposite
the obtuse angle.
Click here to download the GSP file for the images
above. Drag and click on a vertex to change the shape of the triangle and
notice the different positions of the Orthocenter.
So, to summarize our findings, We make the following statements:
1. For an acute triangle, the orthocenter (H) will always lie at some point
on the interior of the triangle.
2. For a right triangle, the orthocenter will lie on the vertex of the right
angle.
3. For an obtuse triangle, the orthocenter will lie on the extension of
the altitude to the side opposite the obtuse angle.
Return to Bill Tankersley's EMT
668 Page