
Bill Tankersley's EMT 668 Page
Write-up 6
Assignment 6 - Problem 1
An Exploration with Geometer's Sketchpad
Problem: Construct a triangle and its medians. Construct a second triangle
with the three sides having the lengths of the three medians from the first
triangle. Find some relationship between the two triangles. Prove whatever
you find.
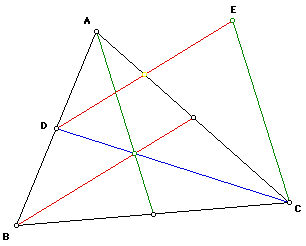
To begin the investigation, I constructed triangle ABC and its triangle
of medians, which is triangle CDE:
Click here to see the GSP file for the drawing
above.
I was interested in investigating the areas of both triangles, and trying
to form some hypothesis and subsequent proof of my findings. After measuring
the areas of both triangles and calculating their ratios, I noticed that
the ratio was always 3 to 4. In other words, the area of triangle CDE is
always 3/4 the area of triangle ABC. Notice the constant ratio of the areas
(.75) as you click and drag on any vertex of triangle ABC.
Next, I was interested in proving this relationship between the two triangles.
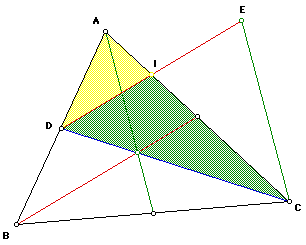
To begin a proof, I constructed point I, which is the intersection of segments
AC and DE. The next task was to construct polygon interiors (triangles)
IDC and ADC. Notice that the area of triangle IDC must be 1/2 the area of
triangle CDE, and that the area of triangle ADC must be 1/2 the area of
triangle ABC. We know this is true since the medians of a triangle bisect
each of the sides.
Click here to see the GSP file for the drawing
above. After calculating the ratios of the areas of triangles IDC and ADC,
we find that the ratio is again 3 to 4. Since this is true, we know that
the areas of triangles ABC and CDE must be in the ratio 3 to 4, since the
new triangles are exactly half the area of the original triangles. Although
this may not be considered a thorough proof, it gives us better insight
into why the ratio of areas of triangle ABC and triangle CDE is 3 to 4.
Another relationship between the triangles that I wanted to investigate
was the ratio of their perimeters. Click here
to see a GSP file of the two triangles with the measures of their perimeters.
Notice that as you click and drag a vertex of triangle ABC, the ratio of
the areas stays around .86 or .87, until we make some drastic changes in
the appearance of the triangles. We quickly see that the ratios of their
perimeters is not constant.



