

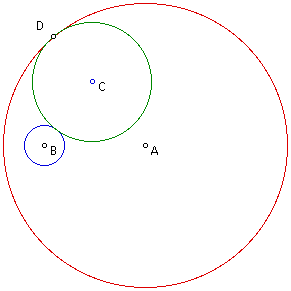
Click here to see a GSP file of the drawing
above. Click on animate to determine the locus of point C, the center of
the tangent circle. You should find that the locus is an ellipse.
Next, let's examine the case where the two circles are disjoint:
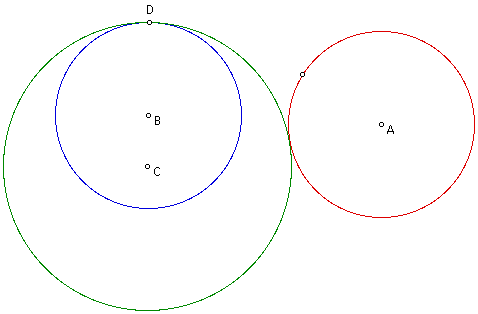
In the drawing above, the circles with centers A and B are constructed
first, then the circle with center C is the tangent circle to the two existing
circles. To find out what the locus of points will be for the center of
the tangent circle, click here to download a
sketch and click on the animate button. You should find that the locus is
a hyperbola.
Next, let's examine the case where the two given circles are intersecting:
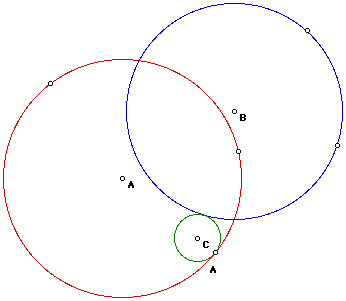
Click here to see a GSP file of the drawing
above. Click on animate to determine the locus of point C. You should find
that the locus is an ellipse again.
A somewhat trivial but interesting case of the tangent circles is when the
two given circles are tangent to each other. In this case, the tangent circle
to the two circles is one of the given circles themselves.
One of the interesting things about this assignment is trying to prove why
we get an ellipse and a hyperbola for the locus of points of the center
of the tangent circle. For an ellipse, we have that the sum of the distances
from the foci to a point on the ellipse is always a constant. For the hyperbola,
the difference to the two distances from a point on the hyperbola to the
foci is a constant.
After observing some of the sketches and animations above, hopefully you
can see that the foci of the ellipse and hyperbola are always the centers
of the two given circles. Because the two given circles do not move, we
have the fixed distances that we need for the construction of an ellipse
and hyperbola.
Click here to download a GSP script for the tangent
circle.