
Bill Tankersley's EMT 668 Page
Write-up 9
Pedal Triangles
Let triangle ABC be any triangle. Then is P is any point in the plane,
the triangle formed by constructing perpendiculars to the sides of ABC (extended
if necessary) locate three points R,S, and T that are the intersections.
Triangle RST is the Pedal Triangle for Pedal Point P.
Click here to download a GSP script for the general
construction of a pedal triangle RST to triangle ABC where P is any point
in the plane of ABC.
Click here to download a GSP sketch of a pedal triangle
RST to triangle ABC where P is any point in the plane of ABC.
Below is a drawing of a Pedal Triangle RST to triangle ABC for Pedal Point
P:
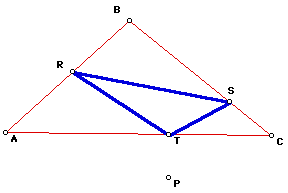
For this write-up, I would like to concentrate on the following question:
What if P is one of the vertices of triangle ABC?
To aid in this investigation, I took the above drawing and moved Pedal Point
P so that it coincides with vertex A:
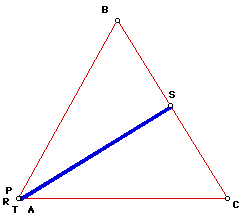
After moving Pedal Point P to coincide with vertex A, I measured angle BSA,
which turned out to be 90 degrees. Therefore, I think that if Pedal Point
P coincides with a vertex of triangle ABC, the Pedal triangle collapses
into the altitude from the vertex to the opposite side. Let's see if we
get the same results when moving Pedal Point P to coincide with vertex C:
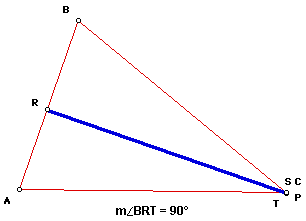
Again, we see the collapsing of the pedal triangle and that measure
of angle BRT is 90 degrees. The other case would be to move Pedal Point
P to coincide with vertex B, which will be left to the reader. After downloading
the GSP file for the pictures above, click and drag Pedal Point P to coincide
with vertex B and measure the angle formed.
Return to Bill Tankersley's EMT 668 Page




