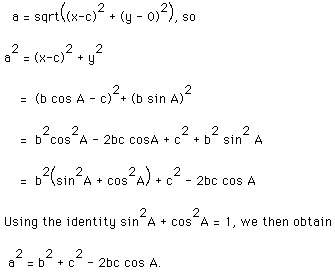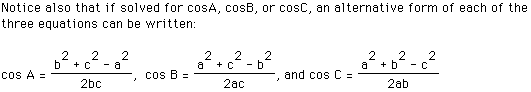Department of Mathematics Education
EMT 669, J. Wilson

---

An Instructional Unit

on

The Law of Sines

and

The Law of Cosines

Introduction

Having taught trigonometry in a high school setting for the past two years, I have experience with teaching the Law of Sines and the Law of Cosines. Although both laws are different in their appearance, they both essentially serve similar purposes, which is finding missing angle measures and side lengths of triangles. Technology can play an enormous role in helping students gain a better understanding and appreciation for the proof as well as the application of the two laws. My goal here is to present about two weeks worth of material on the two laws, which relies on technology as the primary method of instruction. Since we are dealing with triangles, I will specifically focus on the use of Geometer's Sketchpad for the unit. I find that GSP works really well for the purpose of demonstrations. For this unit, I will give some practice problems and a quiz on the two laws separately. The two quizzes could be merged together to form a unit test if desired. The unit could be supplemented with additional practice problems if necessary. The solutions to the practice problems and quizzes will be located on a separate web page which will be linked back to this page.

---

We begin our new unit by examining the following diagram:

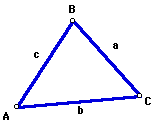
This is an example of an oblique triangle, which is a triangle with no right angles. Although this particular oblique triangle has all acute angles, we could just as well have an oblique triangle with an obtuse angle, as shown below:

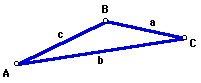
Recall that to "solve" a triangle means to find all three side lengths as well as each of the angle measures. We have already learned how to solve right triangles, so now we are going to learn how to do the same thing with oblique triangles. Also recall that as standard notation, we label the angles of a triangle as A, B, and C, and their opposite sides as a, b, and c.

To solve an oblique triangle, we need to know the measure of at least one side and any two other parts of the triangle - either two sides, two angles, or one angle and one side. This breaks down into the following four possible cases:

1. Two angles and any side (AAS or ASA)
2. Two sides and any angle opposite one of them (SSA)
3. Three sides (SSS)
4. Two sides and their included angle (SAS)

You may be wondering why there is no AAA in the list above. In other words, why can we not solve an oblique triangle if the only information we know is the measures of its three angles? The answer to this may not be obvious until you actually look at a couple of triangles, shown below:

Both of these triangles have the same exact angle measures, which happen to be 60 degrees for each angle. Therefore, simply giving three angle measures in a triangle does not uniquely determine the side lengths of the triangle. There are infinitely many triangles whose angles measure 60 degrees, or any other number of degrees.

---

Examples

Let's look at an example problem now. Suppose we had a triangle with C=102.3 degrees, B=28.7 degrees, and b=27.4 feet, as shown below:

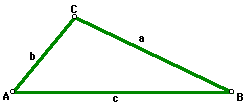
How could we go about finding the measure of the remaining angle and sides? Well, if we remember that the sum of the interior angles of a triangle is 180 degrees, then we could add up the two given angle measures and subtract from 180, leaving us with a measure of 49 degrees for angle A. How about the measures of sides a and c?

To help solve this triangle and many others like it, let's examine the following diagram:

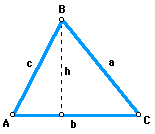
Here, we see triangle ABC and the altitude from angle B to side b, labeled h. Let's look at a couple of trigonometric ratios involving angles in the above triangle:

sin A = h / b

sin C = h / a

If we solve both of these equations for h, we get the following:

a * sin C = c * sin A

After manipulating this equation, we can make the following statement:

(a / sin A) = (c / sin C)

Note that neither sin A nor sin C can equal 0, since no angle of a triangle can have a measure of 0 degrees or 180 degrees.

In a similar manner, if we constructed an altitude from vertex C to side c, we can show the following:

(a / sin A) = (b / sin B)

Therefore, we can conclude that the following statement is true:

(a / sin A) = (b / sin B) = (c / sin C)

Likewise, the following must be true:

(sin A / a) = (sin B / b) = (sin C / c).

Both of these statements are known as the Law of Sines.

Click here to examine a sketch of the Law of Sines. Click and drag on any vertex of triangle ABC and watch the values change, maintaining the equalities stated by the Law of Sines.

Now, let's return to the example problem above, where we were finding the remaining side lengths of triangle ABC. By the Law of Sines, we have:

(a / sin A) = (b / sin B)

(a / sin 49) = (27.4 / sin 28.7)

Solving for a, we find that a = 43.06 feet. Likewise, to find c, we have:

(b / sin B) = (c / sin C)

(27.4 / sin 28.7) = (c / sin 102.3)

This leads to finding that c = 55.75 feet. It is always important to sketch the triangle and check for feasibility of the answers. Remember that the longest side lies opposite the largest angle, and the shortest side lies opposite the smallest angle of a triangle.

Now, let's stop and analyze the Law of Sines and come up with an understanding of the givens we must have in order to use the Law of Sines. Since the Law of Sines involves two angle measures and two side lengths, we know that if we are only given the measures of three sides of a triangle, SSS, the Law of Sines is unable to help us in this situation. Likewise, if we are given two sides and their included angle, SAS, we will again be unable to use the Law of Sines to solve the triangle. (Think about it for a minute!!) Therefore, the Law of Sines only works for the following two cases, mentioned at the beginning of the unit:

1. Two angles and any side (AAS or ASA)
2. Two sides and any angle opposite one of them (SSA)

We have already seen an example of #1 above, which was AAS. Let's look at an example given ASA:

A pole tilts toward the sun at an 8 degree angle from the vertical, and it casts a 22-foot shadow. The angle of elevation from the tip of the shadow to the top of the pole is 43 degrees. How tall is the pole?

First, we need a drawing of the situation. Let's have side a represent the pole:

Note that A = 43 degrees, and B = 90 degrees + 8 degrees = 98 degrees. Thus, angle C = 180 - (43+98)= 39 degrees. Using the Law of Sines, we have:

(a / sin A) = (c / sin C)

(a / sin 43) = (22 / sin 39)

Thus, a = 23.84 feet.

Now, our last example of the Law of Sines involves a triangle for which we were given two side lengths and an angle measure opposite one of the sides. Before we start the example, let's try the following activity:

Sketch a triangle ABC such that a=12 meters, b=31 meters, and A=20.5 degrees.

After giving this activity to students, you may be surprised at the results. Some students may draw a triangle that looks like the following:

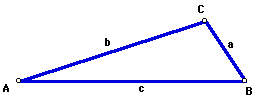
After measuring each of the angles and side lengths, we see that this is definitely a valid triangle. Next, some students may draw a triangle that looks like the following:

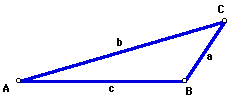
Wait a minute!!! This is also a valid triangle for the given information. How did this happen???? It looks like there are two distinct triangles that can be drawn from the given information. Wow, this SSA thing looks like a lot of trouble. (Gotta be careful how we spell SSA, too, huh?) This leads to the following discussion.

---

SSA (The Ambiguous Case)

There are three possible situations that can occur when you are given two side measures and one opposite angle measure of a triangle:

1) No such triangle exists
2) One such triangle exists
3) Two distinct triangles may satisfy the conditions. (This is the case we just observed.)

Let's begin to make some sense out of this. Here are some criteria that will help you determine the possibilities:

Let's refer to the angle we are given as angle A, which is either acute or obtuse.

If A is acute, we have the following:

1) if a < h, there is no such triangle
2) if a = h or if a>h, there is one such triangle
3) if h < a < b, there are two such triangles

If A is obtuse, we have the following:

1) if a < h or if a = h, there is no such triangle
2) if a > h, there is one such triangle

Recall that in order to calculate the value of h, we use the equation h = b sin A.

---

Let's look at another example of the SSA case. Suppose we are given a triangle such that a = 10 in., b = 12 in., and A = 62 degrees. Determine the number of possible triangles.

Let's first calculate the value of h. Since h = b sin A, we have h = 12 * sin 62 degrees = 10.6

Now, we know that A is acute and a < h. This tells us that there is no such triangle.

---

Let's try one more. Suppose we are given a triangle such that A = 98 degrees, a = 10, and b = 3. Determine the number of possible triangles.

We have h = b Sin A = 10 * sin 98 degrees = 9.9

Therefore, we have that a > h and A is acute, so there is one such triangle.

Remember that it is important to sketch the triangle to make sure that the result is feasible.

---

Practice Problems - Law of Sines

Quiz - The Law of Sines

Recall that the Law of Sines requires that either two angle measures and one side length (ASA and AAS) be known or two side lengths and an angle opposite one of the sides be known. This leaves the SSS and SAS cases still unsolvable.

Consider the following diagram:

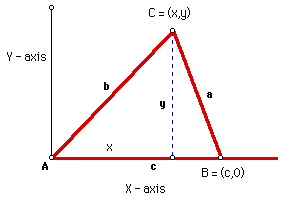
In the figure, note that point B has coordinates (c,0). Furthermore, C has coordinates (x,y),
where x = b cos A and y = b sin A. Since a is the distance from vertex C to vertex B, it follows from the distance formula that:



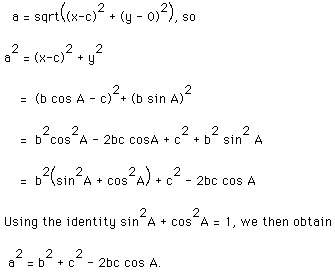
This result is known as the Law of Cosines.



Click here to examine a sketch of the Law of Cosines. Click and drag on any vertex of triangle ABC and watch the values change, maintaining the equalities stated by the Law of Cosines.

It is quite interesting here to note that if angle A measures 90 degrees in the drawing above, then
cos A = 0, and we have the Pythagorean Theorem, 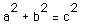. Thus, it appears that the Pythagorean Theorem is just a special case of the Law of Cosines.




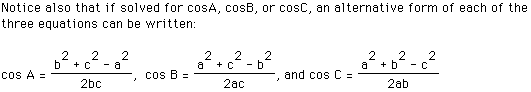
Now, we will see a couple of examples of the Law of Cosines. Remember that we will use the Law of Cosines when we are given SSS or SAS.

Find the three angles of a triangle whose sides have lengths a = 8 feet, b = 19 feet, and c = 14 feet.

It is wise to find the measure of the largest angle first, for this determines the size of the remaining angles.

From the law of Cosines, we have the following:

cos B = (8*8 + 14*14 - 19*19)/ (2*8*14) = -.45089

Since cos B is negative, you know that B must be obtuse, since cosine is negative in the second and third quadrants. Using the inverse cosine function, we see that B = 116.8 degrees. At this point, we could use the Law of Cosines again to find the measures of angles A and C, however it is simpler to revert back to the Law of Sines to obtain the following:

sin A = 8 * (sin 116.8 / 19) = 0.37582. Since angle B was obtuse, A and C must be acute.

Thus, A = 22.08 degrees and C = 180 - 22.08 - 116.8 = 41.12 degrees.

Next, let's try an example of SAS.

The pitcher's mound on a softball field is 46 feet from home plate and the distance between the bases is 60 feet. How far is the pitcher's mound from first base?

Let's look at a diagram for the problem:

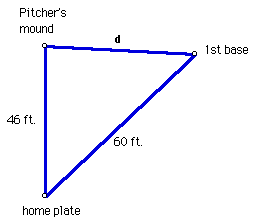
We know that the angle formed at home plate is 45 degrees, since the line from the pitcher's mound to home plate bisects the angle formed by the first base line and the third base line. Using the Law of Cosines, we get the following:

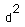= 46*46 + 60*60 - 2*46*60*cos 45 degrees = 1812.8

Therefore, the approximate distance (d) between the pitcher's mound and 1st base is:

d = 42.58 feet.

---

Practice Problems - Law of Cosines

Quiz - Law of Cosines

1. A triangular parcel of land has 375 feet of frontage, and the other boundaries have lengths of 250 feet and 300 feet. What angles does the frontage make with the two other boundaries?

2. In order to determine the distance between two aircraft, a tracking station continuously determines the distance to each aircraft and the angle A between them. Determine the distance a between the planes when A = 42 degrees, b = 35 miles, and c = 20 miles.

3. Refer to the example above involving the softball diamond. On a baseball field, the bases are 90 feet apart and the pitcher's mound is 60 feet from home plate. a) How far is it from the pitcher's mound to third base? b)When a runner is halfway from second to third, how far is the runner from the pitcher's mound?

4. Use the Law of Cosines to find the missing information: a = 1.42, b = 0.75, c = 1.25