Assignment 12
Using excel spreadsheets in the classroom
Use the following exploration to generate a function to predict observed
data.
a.Take a cup of hot water and measure its initial temperature (time
= 0) and then record temperature readings each minute for 30 minutes. Make
note of the room temperature . . .
b. Enter the data on a spread sheet and construct a function that
will model the data.
c. Using the function predict the temperature after 45 minutes, 60
minutes, or 300 minutes.
d. Calculate a measure of the error between your model and the observed
data by taking the square of the difference for each time, sum the squares,
and divide by the number of data points. You can use this statistic to guide
refinement of your function to model the data.
The following write-up is a simulation of a lab
that can be implemented in a mathematics or science classroom.
Situation: You have recently been assigned as the vice-president
in charge of containers at Coffee Unlimited, the hottest and newest coffee
hangout that is sweeping the nation with its 150 coffee flavors. The sudden
success is attributed to your most popular flavor: Chocolate Chip Mint Coffee.
With the increase of sales, a natural way to advertise your name is to create
coffee cups with your name on them.
Your assignment to find the best container for coffee....this
means you must find a material that will hold the heat of the coffee for
as long as possible!!! Good Luck and Happy Brewing.
Materials:
1. Containers made of various materials. (styrofoam, ceramics,
paper, stainless steel)
2. Thermometers (candy or high temperature thermometers
work best for this lab)
3. Water
4. Heating burner (bunson burner)
5. Pan(beaker)
6. Timer
7. Spreadsheet program
Procedure:
1. Collect different containers (at least three) that are
made of different materials to bring in to class.
2. Heat the water in your pan or beaker....bringing the
water to a boil. The temperature of your starting temperature should be
approximately 212 degrees fahrenheit (100 degrees celsius).
3. Measure its initial temperature (time = 0) and then
record temperature readings each minute for 30 minutes. Make note of the
room temperature . . .
4. Enter the data on a spread sheet and construct a function
that will model the data.
5. Using the function predict the temperature after 45
minutes, 60 minutes, or 300 minutes.
6. Calculate a measure of the error between your model
and the observed data by taking the square of the difference for each time,
sum the squares, and divide by the number of data points. You can use this
statistic to guide refinement of your function to model the data.
7. Repeat with each container.
8. Construct graphs for each container, and thus for each
function/data in the spreadsheet.
Analysis/Assessment:
Use the data, function, and graphs to present an argument
for your coffee cups. Your information should be presented in a clear manner
and in the form of a "report" to your boss.
Here is an example of data that was collected for
three different containers.
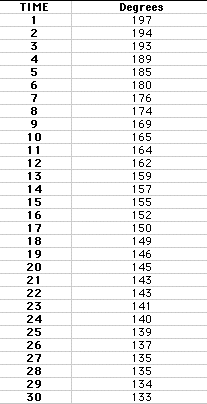
Container #1: Stainless Steel Camping Mug
Note: The initial temperature for each of the experiments
never reached 212 degrees when it was transferred out of the heating container.
As you can see the stainless steel mug held the temperature
of the water extremely well. After 30 minutes, the temperature was still
above 130 degrees. We can use a function to describe this data that will
help predict the temperature at future times. It is an exponential decreasing
function with relation to time. Using a spreadsheet and graph will help
create the function. The function will be most accurate when its graph looks
like the graph of the data. The function that best 'fits' the set of data
is:
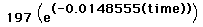
| Data from Excel Spreadsheet |
| TIME |
DEGREES |
FUNCTION |
Difference of Temp |
Difference Squared |
| 1 |
197 |
193.778921899137 |
3.22107810086277 |
10.3753441318577 |
| 2 |
194 |
190.63953942136 |
3.36046057864002 |
11.2926953005936 |
| 3 |
193 |
187.57978053531 |
5.42021946468975 |
29.3787790454017 |
| 4 |
189 |
184.597625762188 |
4.40237423781207 |
19.3808989297514 |
| 5 |
185 |
181.691106842869 |
3.3088931571306 |
10.9487739253057 |
| 6 |
180 |
178.858305438832 |
1.14169456116753 |
1.30346647099951 |
| 7 |
176 |
176.097351866029 |
-0.0973518660289017 |
0.00947738581930922 |
| 8 |
174 |
173.40642386087 |
0.593576139130107 |
0.352332632944604 |
| 9 |
169 |
170.783745377509 |
-1.7837453775094 |
3.18174757178617 |
| 10 |
165 |
168.227585415632 |
-3.22758541563203 |
10.4173076152006 |
| 11 |
164 |
165.736256877971 |
-1.73625687797124 |
3.01458794630245 |
| 12 |
162 |
163.308115456804 |
-1.30811545680427 |
1.71116604833025 |
| 13 |
159 |
160.941558548689 |
-1.94155854868865 |
3.76964959798597 |
| 14 |
157 |
158.635024196724 |
-1.63502419672398 |
2.67330412387288 |
| 15 |
155 |
156.386990059641 |
-1.38699005964125 |
1.92374142554364 |
| 16 |
152 |
154.195972407038 |
-2.19597240703843 |
4.82229481247414 |
| 17 |
150 |
152.0605251401 |
-2.06052514010017 |
4.24576385298482 |
| 18 |
149 |
149.979238837155 |
-0.979238837154696 |
0.958908700192082 |
| 19 |
146 |
147.950739823438 |
-1.95073982343791 |
3.80538585874658 |
| 20 |
145 |
145.973689264451 |
-0.973689264451082 |
0.948070783707289 |
| 21 |
143 |
144.046782282313 |
-1.04678228231347 |
1.0957531465654 |
| 22 |
143 |
142.168747094527 |
0.831252905473207 |
0.690981392857648 |
| 23 |
141 |
140.338344174583 |
0.661655825417199 |
0.437788431308515 |
| 24 |
140 |
138.554365433861 |
1.44563456613923 |
2.08985929881657 |
| 25 |
139 |
136.815633424274 |
2.18436657572624 |
4.77145733715 |
| 26 |
137 |
135.121000561138 |
1.87899943886168 |
3.53063889124252 |
| 27 |
135 |
133.469348365754 |
1.5306516342456 |
2.34289442541873 |
| 28 |
135 |
131.859586727196 |
3.14041327280435 |
9.86219552400574 |
| 29 |
134 |
130.290653182822 |
3.7093468171775 |
13.7592538101049 |
| 30 |
133 |
128.761512217044 |
4.23848778295624 |
17.9647786862693 |
|
|
|
|
|
|
|
|
|
|
| 45 |
|
109.970316313254 |
|
ERROR |
| 60 |
|
97.1883095908172 |
|
5.43648394724235 |
| 120 |
|
75.8205053417805 |
|
|
| 180 |
|
71.2460606394278 |
|
|
| 240 |
|
70.2667581293992 |
|
|
| 300 |
|
70.057107894551 |
|
|
|
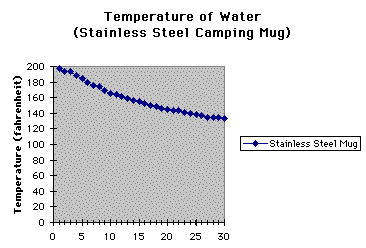
The function and the data help to predict the temperature
at 45 minutes, 1 hour, 2 hours, 3 hours, 4 hours, and 5 hours. Please note
that the temperature of the water is close to 100 degrees after an hour.
Below is a graph of the data and the function.
The error of the function was determined by squaring the
difference of the temperatures, finding the sum of the squares and by dividing
by the number of temperature readings. The error for this function was approximately
5.4365. The error should be close to zero in order for the function to be
a reasonable estimate.
Container #2: Ceramic Mug
Note: The initial temperature for each of the experiments
never reached 212 degrees when it was transferred out of the heating container.
TEMPERATURE OF WATER
| TIME |
DEGREES |
| 1 |
187 |
| 2 |
176 |
| 3 |
168 |
| 4 |
162 |
| 5 |
156 |
| 6 |
150 |
| 7 |
147 |
| 8 |
142 |
| 9 |
139 |
| 10 |
135 |
| 11 |
133 |
| 12 |
130 |
| 13 |
127 |
| 14 |
125 |
| 15 |
124 |
| 16 |
121 |
| 17 |
119 |
| 18 |
117 |
| 19 |
114 |
| 20 |
113 |
| 21 |
110 |
| 22 |
109 |
| 23 |
107 |
| 24 |
106 |
| 25 |
105 |
| 26 |
105 |
| 27 |
104 |
| 28 |
103 |
| 29 |
101 |
| 30 |
100 |
|
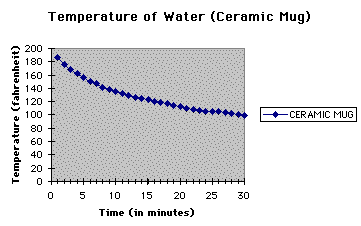
The temperature of the water in the ceramic mug began to
lose heat quite rapidly. After only 30 minutes the temperature was 100 degrees.
Compare that with the stainless steel camping mugs temperature after 30
minutes and 1 hour. Again we can use a function to describe our set of data
points. This will help to predict the temperature at 45 minutes, 1 hour,
2 hours, 3 hours, 4 hours, and 5 hours. The function that best 'fit' this
data is:
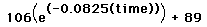
| TIME |
CERAMIC MUG |
FUNCTION |
Difference of Temp |
Difference Squared |
| 1 |
187 |
186.606012412821 |
0.393987587178714 |
0.155226218850905 |
| 2 |
176 |
178.876732633319 |
-2.87673263331908 |
8.27559064360292 |
| 3 |
168 |
171.759523405958 |
-3.75952340595813 |
14.1340162399471 |
| 4 |
162 |
165.205915743784 |
-3.20591574378417 |
10.2778957562432 |
| 5 |
156 |
159.171278849228 |
-3.1712788492284 |
10.0570095395634 |
| 6 |
150 |
153.614516173409 |
-3.61451617340879 |
13.0647271678337 |
| 7 |
147 |
148.497785544058 |
-1.4977855440583 |
2.24336153599003 |
| 8 |
142 |
143.78624145612 |
-1.78624145612011 |
3.19065853956209 |
| 9 |
139 |
139.44779776998 |
-0.447797769980042 |
0.200522842799099 |
| 10 |
135 |
135.452909201285 |
-0.452909201284626 |
0.205126744608278 |
| 11 |
133 |
131.774370114266 |
1.22562988573353 |
1.50216861680317 |
| 12 |
130 |
128.387129248337 |
1.61287075166314 |
2.60135206157042 |
| 13 |
127 |
125.268119116213 |
1.73188088378714 |
2.99941139562733 |
| 14 |
125 |
122.396098911762 |
2.60390108823819 |
6.78030087732802 |
| 15 |
124 |
119.751509857747 |
4.24849014225254 |
18.049668488817 |
| 16 |
121 |
117.31634200838 |
3.68365799161987 |
13.5693361992249 |
| 17 |
119 |
115.074011599582 |
3.92598840041845 |
15.4133849202202 |
| 18 |
117 |
113.009248111706 |
3.99075188829431 |
15.9261006339246 |
| 19 |
114 |
111.1079902756 |
2.89200972439951 |
8.36372024602136 |
| 20 |
113 |
109.3572903138 |
3.64270968620006 |
13.2693338579358 |
| 21 |
110 |
107.745225764719 |
2.25477423528149 |
5.08400685208922 |
| 22 |
109 |
106.260818289361 |
2.73918171063913 |
7.50311644389991 |
| 23 |
107 |
104.893958907611 |
2.10604109238858 |
4.43540908282928 |
| 24 |
106 |
103.635339154955 |
2.36466084504536 |
5.59162091209066 |
| 25 |
105 |
102.476387690796 |
2.52361230920422 |
6.36861908716708 |
| 26 |
105 |
101.409211926677 |
3.5907880733226 |
12.8937589875158 |
| 27 |
104 |
100.426544276874 |
3.57345572312639 |
12.7695858051447 |
| 28 |
103 |
99.5216926653224 |
3.47830733467757 |
12.0986219144718 |
| 29 |
101 |
98.688494951843 |
2.31150504815704 |
5.3430555876555 |
| 30 |
100 |
97.9212769672749 |
2.07872303272509 |
4.32108944678181 |
|
|
|
|
|
| 45 |
|
91.5881390245552 |
|
ERROR |
| 60 |
|
89.7508413464795 |
|
7.74555690664458 |
| 120 |
|
89.005318516298 |
|
|
| 180 |
|
89.0000376732258 |
|
|
| 240 |
|
89.0000002668549 |
|
|
| 300 |
|
89.0000000018902 |
|
|
|
The error of the function was determined by squaring the
difference of the temperatures, finding the sum of the squares and by dividing
by the number of temperature readings. The error for this function was approximately
7.7456. The error should be close to zero in order for the function to be
a reasonable estimate.
Using the function we can predict that the temperature
will reach room temperature after an hour. Substituting 60 minutes in for
the value of t (time), we can predict that it will reach room temperature
in an hour.
Note: The room temperature may seem a bit high, but the
experiment was performed close to a vent in a small studio apartment when
the heat began to heat the air.
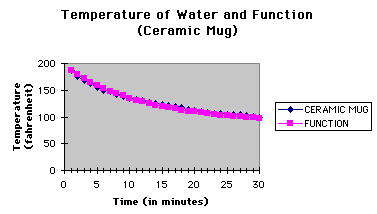
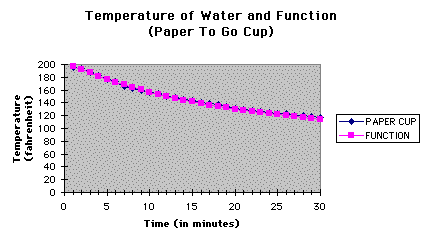
Container #3: Paper (to go) Cup
Note: The initial temperature for each of the experiments
never reached 212 degrees when it was transferred out of the heating container.
TEMPERATURE OF WATER
| TIME |
PAPER CUP |
| 1 |
195 |
| 2 |
194 |
| 3 |
187 |
| 4 |
183 |
| 5 |
176 |
| 6 |
173 |
| 7 |
166 |
| 8 |
163 |
| 9 |
160 |
| 10 |
156 |
| 11 |
154 |
| 12 |
150 |
| 13 |
148.5 |
| 14 |
145 |
| 15 |
143 |
| 16 |
141 |
| 17 |
139.5 |
| 18 |
137.5 |
| 19 |
135 |
| 20 |
131 |
| 21 |
129 |
| 22 |
128 |
| 23 |
127 |
| 24 |
125 |
| 25 |
124 |
| 26 |
124 |
| 27 |
121 |
| 28 |
120 |
| 29 |
119 |
| 30 |
117 |
|
The paper (to-go) cup held much of the temperature of the
water. It is interesting to note that there were times when the temperature
was held constant for a couple of minutes. Although it does not hold heat
as well as the stainless steel camping mug it performed better than the
ceramic mug.
| TIME |
DEGREES |
FUNCTION |
Difference of Temp |
Difference Squared |
| 1 |
195 |
197.613366274883 |
-2.61336627488322 |
6.82968328669699 |
| 2 |
194 |
192.041754882618 |
1.95824511738189 |
3.83472393975002 |
| 3 |
187 |
186.768307449671 |
0.231692550329285 |
0.0536814378780883 |
| 4 |
183 |
181.777067775873 |
1.22293222412736 |
1.4955632248091 |
| 5 |
176 |
177.052933554747 |
-1.05293355474652 |
1.10866907071114 |
| 6 |
173 |
172.581610677512 |
0.41838932248811 |
0.17504962517206 |
| 7 |
166 |
168.349569982505 |
-2.34956998250465 |
5.52047910268689 |
| 8 |
163 |
164.344006319146 |
-1.34400631914554 |
1.80635298590313 |
| 9 |
160 |
160.552799802594 |
-0.552799802594024 |
0.305587621747991 |
| 10 |
156 |
156.964479141854 |
-0.964479141853531 |
0.930220015070523 |
| 11 |
154 |
153.568186930368 |
0.431813069631971 |
0.186462527104986 |
| 12 |
150 |
150.353646794087 |
-0.353646794086899 |
0.125066054967941 |
| 13 |
148.5 |
147.311132297596 |
1.18886770240351 |
1.41340641381821 |
| 14 |
145 |
144.431437514235 |
0.568562485764915 |
0.323263300219179 |
| 15 |
143 |
141.705849171144 |
1.29415082885558 |
1.67482636782758 |
| 16 |
141 |
139.126120284974 |
1.87387971502605 |
3.51142518638611 |
| 17 |
139.5 |
136.684445208467 |
2.81555479153297 |
7.92734878412429 |
| 18 |
137.5 |
134.373436012425 |
3.12656398757497 |
9.77540236840069 |
| 19 |
135 |
132.186100131587 |
2.81389986841265 |
7.91803246945272 |
| 20 |
131 |
130.115819206789 |
0.884180793211272 |
0.781775675083713 |
| 21 |
129 |
128.156329059375 |
0.84367094062452 |
0.711780656054262 |
| 22 |
128 |
126.301700737288 |
1.6982992627124 |
2.88422038572947 |
| 23 |
127 |
124.546322575458 |
2.45367742454243 |
6.02053290370919 |
| 24 |
125 |
122.884883216244 |
2.11511678375646 |
4.47371900892828 |
| 25 |
124 |
121.312355538522 |
2.68764446147789 |
7.22343275131276 |
| 26 |
124 |
119.823981446813 |
4.17601855318699 |
17.439130956562 |
| 27 |
121 |
118.415257474412 |
2.58474252558844 |
6.6808939235853 |
| 28 |
120 |
117.081921156968 |
2.91807884303242 |
8.51518413415342 |
| 29 |
119 |
115.81993813528 |
3.18006186472016 |
10.1127934634475 |
| 30 |
117 |
114.625489948283 |
2.37451005171704 |
5.63829798570525 |
|
|
|
|
|
| 45 |
|
102.757928928304 |
|
ERROR |
| 60 |
|
97.5571484141364 |
|
3.99195692137645 |
| 120 |
|
93.6496404841303 |
|
|
| 180 |
|
93.5055192150262 |
|
|
| 240 |
|
93.5002035661317 |
|
|
| 300 |
|
93.5000075081637 |
|
|
|
It is predicted that the water will reach room temperature
between 45 and 60 minutes, approximately the same time as the ceramic mug.
However, the paper cup does hold the heat a bit longer. It might be interesting
to use the function to look at what is happening between 30 and 45 minutes
comparing the ceramic mug and the paper (to go) cup. The function that best
'fits' this set of data is:
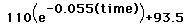
The error of the function was determined by squaring the
difference of the temperatures, finding the sum of the squares and by dividing
by the number of temperature readings. The error for this function was approximately
3.992. The error should be close to zero in order for the function to be
a reasonable estimate.
Note: The room temperature may seem a bit high, but the
experiment was performed close to a vent in a small studio apartment when
the heat began to heat the air.
Conclusion: Using the data and the functions, the recommendation
to the CEO of Coffee Unlimited should be to market Coffee Unlimited Coffee
Mugs made of Stainless Steel.
Return to home page