Part #1
We should start this investigation by first looking at a graph of the equation
We will let a=1 ,b=1, and c=1.
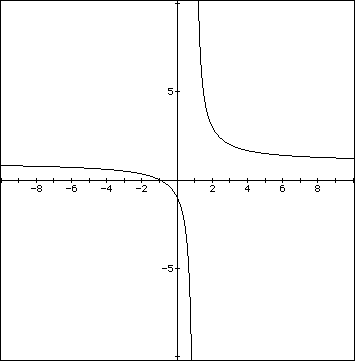
We have a graph that has a vertical asymptotes at x=1 and a horizontal asymptotes
at y=1. We should now vary one of the coefficient and let the other two
remain the same and figure out they are doing. We let a=1, b=1, and let
c vary
By looking at the following graph, we see that the -(c) value is where
the graph of the equation crosses the x axis and y axis. I did not notice
that before. We still have horizontal and vertical asymptotes at y=1 and
x=1 respectively.
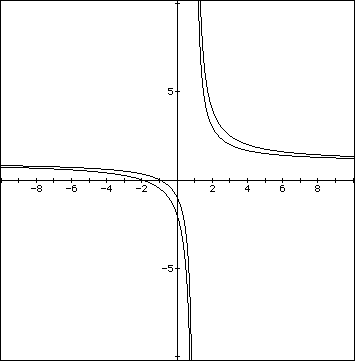
I will check for a few more value of c.
I believe that it will cross the y axis at the negative of the c but not
the x all the time. When the asymptotes are changed where it crossed the
x axis change. After looking at quite a few examples, I came to the conclusion
that the graph will cross the x axis at the negative of c/a.
We need to look at b next we will let a=1 and let c=1 while we vary b.
The following is a graph of b=1 and b=2.
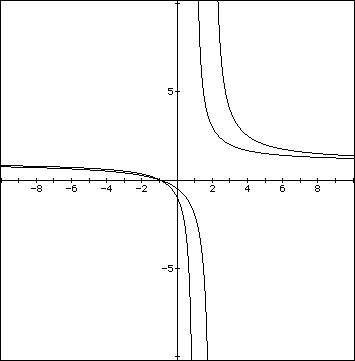
We can tell that the vertical asymptote has been changed from x=1 to
x=2. We should try a few more value to make sure that this is the case
with b. I have checked various cases and this does seem to be the situation.
The b value controls the vertical asymptote.
Now we should let "a" vary and we will let b=1, and c=1. After
looking at several graphs, I have concluded that the value of "a"
will be the horizontal asymptote.
Hence:
a--controls the horizontal asymptotes
b--controls the vertical asymptotes
c--(-c/a) x intercept
The next step in this problem is to ask "what if?". What
I wanted to know was what would happen if we changed to problem and maybe
added a few coeficient.
Doesn't this look like fun? For what values can this be graphed? For what
values will this look like the intesection of straight line? What values
should be considered together to create families of curves?