Problem: Explore problems of maximization such as the lidless box formed
form a 5x8 sheet with a square removed from each corner.
This is a problem that deals with maximizing the volume of a rectangular
solid given a fixed area to work with. Using Excel, I created the following
spreadsheet. I started with a height = .1 . Then I increased the height
by .1 each time. We can tell by the spread sheet that the maximum area will
be attained when the height =1, this will make the length 6 and the width
3. The volume at this point will 18.
Maximum volume of 5x8
length width height volume
7.8 4.8 0.1 3.744
7.6 4.6 0.2 6.992
7.4 4.4 0.3 9.768
7.2 4.2 0.4 12.096
7 4 0.5 14
6.8 3.8 0.6 15.504
6.6 3.6 0.7 16.632
6.4 3.4 0.8 17.408
6.2 3.2 0.9 17.856
6 3 1 18
5.8 2.8 1.1 17.864
5.6 2.6 1.2 17.472
5.4 2.4 1.3 16.848
5.2 2.2 1.4 16.016
5 2 1.5 15
4.8 1.8 1.6 13.824
4.6 1.6 1.7 12.512
4.4 1.4 1.8 11.088
4.2 1.2 1.9 9.576
4 1 2 8
3.8 0.8 2.1 6.384
3.6 0.6 2.2 4.752
3.4 0.4 2.3 3.128
3.2 0.2 2.4 1.536
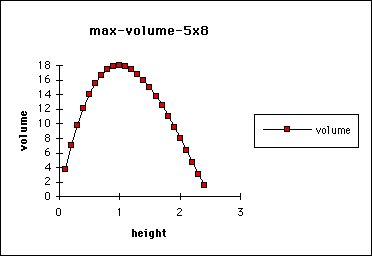
I then wanted to create a graph that showed that this was the maximum volume.
I let the height be the x-axis and the volume be the y- axis. We can see
from the following graph that the maximum is 18 when x=1.

This problem made me wonder what would be the maximum volume if we considered
a 4x8 sheet because that is the dimensions that materials is available.
Therefore I changed a the 5 to a 4 in my first cell in my width column filled
down on that column and I had my answer.
Maximum volume of 4x8
length width height volume
7.8 3.8 0.1 2.964
7.6 3.6 0.2 5.472
7.4 3.4 0.3 7.548
7.2 3.2 0.4 9.216
7 3 0.5 10.5
6.8 2.8 0.6 11.424
6.6 2.6 0.7 12.012
6.4 2.4 0.8 12.288
6.2 2.2 0.9 12.276
6 2 1 12
5.8 1.8 1.1 11.484
5.6 1.6 1.2 10.752
5.4 1.4 1.3 9.828
5.2 1.2 1.4 8.736
5 1 1.5 7.5
4.8 0.8 1.6 6.144
4.6 0.6 1.7 4.692
4.4 0.4 1.8 3.168
4.2 0.2 1.9 1.596
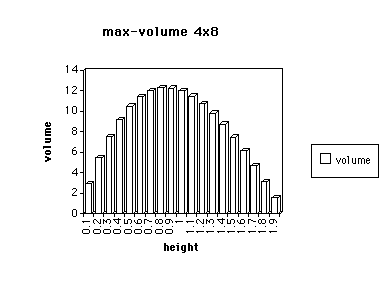
The following graph shows that the maximum volume of a lidless box that
can be created out of a 4x8 sheet will be achieved when the height is a
little less that 1 unit.
The problem that I would like to work on now is maximize the volume of
a box with a lid. We will start of with the dimension of 4x8.
length width height volume
3.9 3.8 0.1 1.482
3.8 3.6 0.2 2.736
3.7 3.4 0.3 3.774
3.6 3.2 0.4 4.608
3.5 3 0.5 5.25
3.4 2.8 0.6 5.712
3.3 2.6 0.7 6.006
3.2 2.4 0.8 6.144
3.1 2.2 0.9 6.138
3 2 1 6
2.9 1.8 1.1 5.742
2.8 1.6 1.2 5.376
2.7 1.4 1.3 4.914
2.6 1.2 1.4 4.368
2.5 1 1.5 3.75
2.4 0.8 1.6 3.072
2.3 0.6 1.7 2.346
2.2 0.4 1.8 1.584
2.1 0.2 1.9 0.798
2 -8.882E-16 2 -3.553E-15
1.9 -0.2 2.1 -0.798
1.8 -0.4 2.2 -1.584
1.7 -0.6 2.3 -2.346
1.6 -0.8 2.4 -3.072
1.5 -1 2.5 -3.75
1.4 -1.2 2.6 -4.368
1.3 -1.4 2.7 -4.914
1.2 -1.6 2.8 -5.376
1.1 -1.8 2.9 -5.742
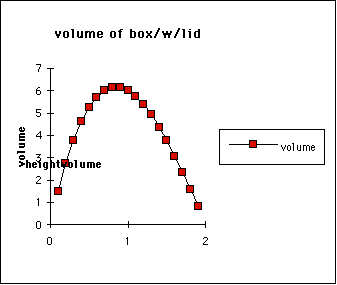
I also created a graph of this
I found this to be a very interesting problem because the spreadsheet
is such a useful tool for exploring formulas and looking a the maximum and
minimum.