Consider the graph of the equation:
For various substitutions of real number coefficients a, b and c.
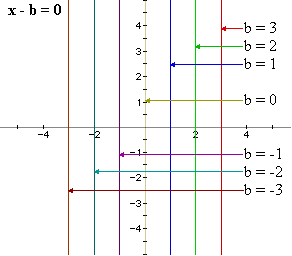
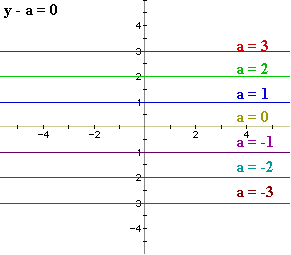
What happens when we consider (x - b)(y - a) = 0 with a = b:
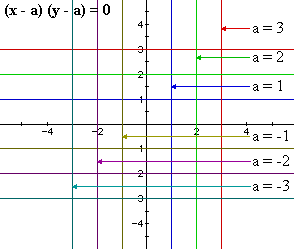
Or (x - b) ( y - a ) = 0 with a not equal to b:
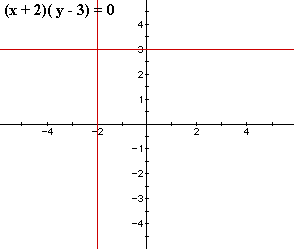
I hope that we are getting a pretty clear picture of what is happening.
The graph of (x - b)(y - a) = 0 seems to give us a "cross" with
a horizontal component equal to the line y = a and vertical component equal
to the line x = b.
Let us now introduce a constant, that is let us consider the graph (x -
b)(y - a) = k:
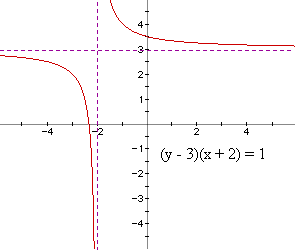
Isn't it amazing what a profound impact a small number like 1 can have!!!
We now have a rectangular hyperbola with asymptotes y = 3 and x = -2.
What is the impact of varying the constant?
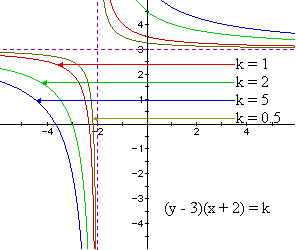
This should not be too surprising!
Let us revisit for a moment rectangular hyperbola (xy = k) that have the
axes as their asymptotes. For k greater than 0 the arms are found in the
first and third quadrants and the arms intersect the line y = x at the point
closest to the origin on each arm - more particularly at the points (sqrt(k),sqrt(k))
and (-sqrt(k), -sqrt(k)). As k increases so will sqrt(k) and the point on
the arms closest to the origin moves further and further from the origin.
(Clearly the case is analogous for k less than zero).
In the example that we have been dealing with we are simply dealing with
this same rectangular hyperbola but have shifted the graph relative to the
axes.
If we now expand the brackets in the equation (y - b)(x - a) = k and transpose
some of the elements we get:
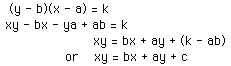
The equation that we wanted to explore in the first place! This equation is then a rectangular hyperbola with asymptotes at y = b and x = a. The quadrants in which the hyperbola lies will depend on the following:
if c + ab is greater than 0 the hyperbola will lie in the first and third quadrants (determined by the shifted axes), and
if c + ab is less than ) the hyperbola will lie in the second and fourth quadrants (determined by the shifted axes).