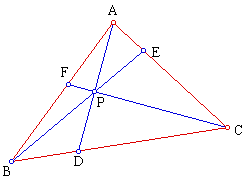
Consider any triangle ABC. Select a point inside the triangle and draw
lines AP, BP and CP extended to meet the opposite sides in D, E and F respectively.

Claim (1):
For all positions of P inside triangle ABC the product (AF)(BD)(AE) will always equal the product (FB)(DC)(EA).
Or more particularly the product of ratios:
Proof of claim (1):
We begin by constructing a line through A that is parallel to BC and meets
lines CF and BE in S and T respectively.
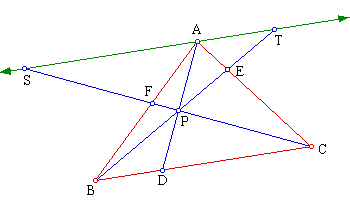
The construction creates a number of similar triangles.
By the pairs of similar triangles SAP and CDP and TAP and BDP:
We can conclude that:![]()
By the pairs of similar triangles TAE and BCE and SAF and CBF:
We can conclude that:![]()
After multiplying we note that:
From whence it follows that (AF)(BD)(AE) = (FB)(DC)(EA)!
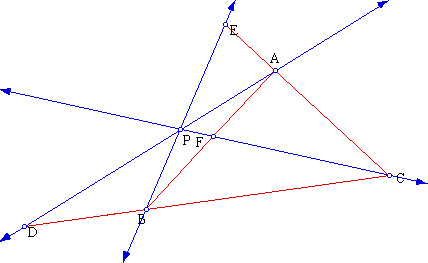
Claim (2):
For all positions of P outside the triangle ABC the product (AF)(BD)(AE) will always equal the product (FB)(DC)(EA).
Clearly the case when P lies on triangle ABC is a trivial case as one of the dimensions in each product goes to zero!
Proof of claim (2):
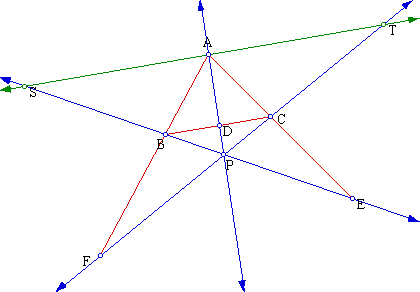
Please note while this is technically the proof of one case - that is
you could argue that there are different possible positions for P, it is
left to the reader to consider the fact that this proof generalises to all
positions of P.
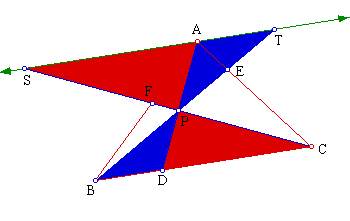
We begin by constructing a line through A that is parallel to BC and meets
lines CF and BE in T and S respectively.
The construction creates a number of similar triangles.
By considering the pairs of similar triangles SAP and BDP and TAP and CDP:
We can conclude that: ![]()
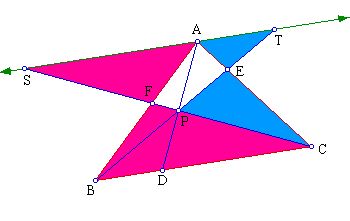
By considering the similar triangles ATF and BCF:
We can conclude that: ![]()
By considering the similar triangles ASE and CBE:

We can conclude that: ![]()
After multiplying we note that:
From whence it follows that (AF)(BD)(AE) = (FB)(DC)(EA)!
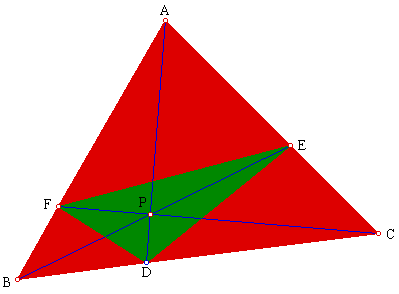
Claim (3):
For all positions of P inside triangle ABC the ratio (area ABC) to (area FED) will always be greater than or equal to 4.