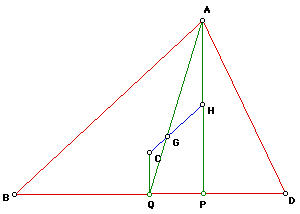

Let C, G be the Circumcenter and Centroid. Produce CG to H so that CG
= one half GH.
It remains to show that H is the Orthocenter.
Join AH and produce it to meet BD at P. Since
and therefore AH is parallel to QC, but CQ is perpendicular to BD and
so AP is an altitude of the triangle. In a similar way DH extended is perpendicular
to AB and H is the orthocenter.