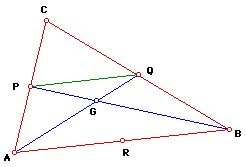

P and Q are the midpoints of AC and BC respectively.
PQ is parallel to and one half the length of AB since it joins the mid-points
of AC and BC.
Hence triangle PGQ is similar to triangle BGA and we have:
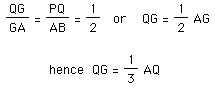
Median BP cuts AQ at the trisection point of AQ closest to Q and similarly
median CR cuts AQ at this same point.