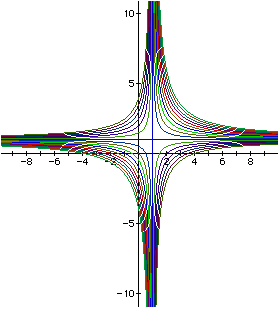

As can be seen by observing this graph, we get hyperbolas when we vary
c and let a=b. When c>=-1/2 the hyperbolas are in the first and third
quadrant and when c<-1/2 they lie in the second and fourth quadrant.
The smaller the value of c; the closer the hyperbolas are to the focal
point or the point of symmetry. The larger the value of c; the further
the hyperbolas lie from the focus or focal point. The focal point is the
intersection of the lines x-a=0 and y-b=0. In our case a=b=1, so our focal
point is the intersection of the lines x=1 and y=1. This point is (1,1).
We also notice that as c gets larger (i.e. the hyperbola moves further from
the focal point) the hyperbolas seem to be getting straighter.
Next, I conducted an investigation to see what happens when a=c=1 and b
varies from -4 to 4. The graph below shows what happens when b is changed.
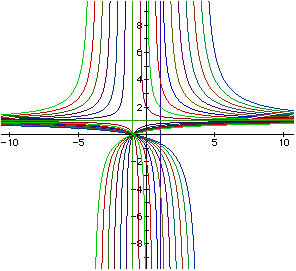
When b is negative, the hyperbolas are formed around the focus point
in quadrants 2 and 4. As b gets larger, the hyperbolas grow closer together
and the focal radius gets smaller and smaller, but the focal point does
not change. During my investigations of these different graphs, I came
across a very interesting graph. The graph of 0=x-y+1-xy.
When I graphed this function ,I did not get the usual hyperbola, I got
what appeared to be perpendicular lines. Now, let's investigate this function
to see why we get this graph. Upon examining this function , 0=x-y+1-xy,
I know that the graph will have a slop of 1-y and a y-intercept of 1. This
also tells us that no matter what value we put in for y, x=-1 and no matter
what value we put in for x, y=1. This explains the perpendicular lines.
This graph is important because as b gets larger the line y=1 seems to
serve as a horizontal asymptote for the hyperbolas. When b is negative,
except for b=-1, the majority of the hyperbolas lie in quadrants 2 and 4.
When b is positive, the hyperbolas lie quadrants 1 and 3. When b is positive,
we get a new focus that never changes. Now as b gets bigger, the focal
radius becomes longer. While investigating these graphs, I also noticed
that they all had one point in common. This point is (-1,0).
Now, we need to see what happens when we let b=c=1 and vary a from -4 to
4. We get the following graphs.
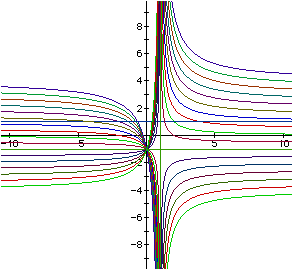
The changes in a are similar to what we observed in the changes of b.
There is one difference though. As we vary a, the focal point also varies.
While a<-1, the focal point does not seem to change and the focal radius
decreased as a got bigger. When a=-1, we get a similar graph as when
b=-1. The graph of 0=-x+y+1-xy also produces perpendicular lines which
serve as vertical and horizontal asymptotes to the other hyperbolas (i.e.
when a>-1). Thus, we have a horizontal asymptote at y=-1 and a vertical
asymptote at x=1. This time they intersect at (1,-1) instead of (-1,1).
As a increased, the pairs of hyperbolas grew further apart and shifted
upward and to the right. As a result of these changes, the focal point
and radius also change. As in the previous cases, when a<-1 the majority
of the hyperbolas tend to lie in the second and forth quadrants and when
a>=-1 they lie in the first and third quadrant. As in the case when
b was varying, the hyperbolas all have one point in common. In this case,
this point is (0,-1).
In conclusion, when c varies the only thing that changes is the focal radii
of pairs of hyperbolas. When b varies, the focal point remains the same
no matter where the hyperbolas are located. When a varies, we get sifting
and turning. The focal point and radius also change when a changes.
To learn more about this problem, there are many extensions that one can
do. One can set the two coefficients that remain constant to be negative
and/or to be different values. Another extension would be to change two
of the coefficients and let the other one remain constant or to change all
three and investigate what happens. These are only a few of the extensions
that one can perform; there are many more.