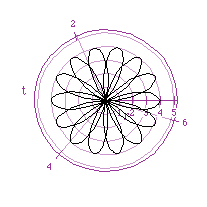

This graph holds for both odd and even values of k. The following is k=6:
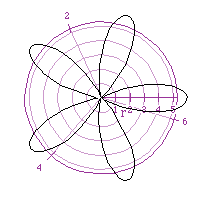
Returning the k value to 5, we can change the relationship of a and b.
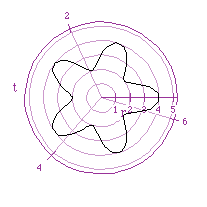
In the case where a>b, the "rose" no longer has a center. Because
the graph does not go into the origin, the "rose" now looks more
like a "starfish".
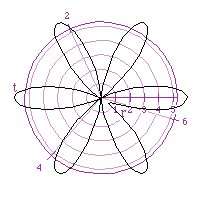
The last relationship with a and b is a<b. In this case we get a smaller
petal within each petal.
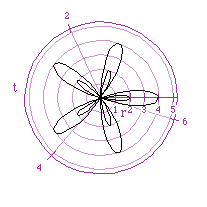
When we go back to a=b, and change the value of k to a rational number
such as 5/2, we get an incomplete "rose":
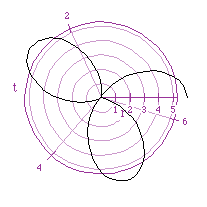
In order to complete this "rose" change the values for t from
0...2 Pi to 0...4.Pi.
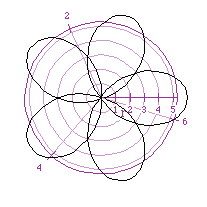
When the value of k is a rational number with a different denominator,
the value of needs to equal 2k Pi.
An interesting graph results when a>b, and k is 5/2:
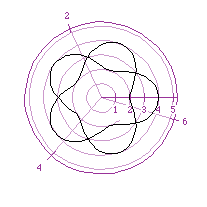
We can now change the function to see if the same effects hold for changes
in b, and k.
The function under investigation is:
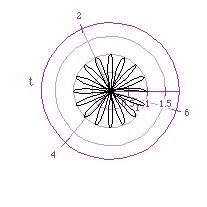
The resulting graphs are much smaller than the previous ones and the
number of pedals equals 2k for even values of k; 1k if k is odd. The size
of the graph can be changed by increasing the values of b.
The following graph is of this function when k is 7, and b is 2.
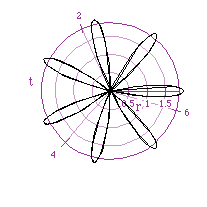
The changing from cos to sin merely changes the orientation of the graph's
pedals.
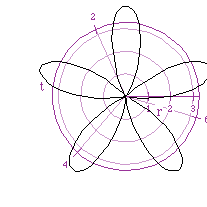
The investigation leads into changingthe function to:
to get the resulting graphs. The a value determined the size of the "rose"
and the k value determined the number of pedals. This graph is when k= 7/2
and the range of t is expaned to 0...4Pi.