PROBLEM:
Given a rectangular sheet of cardboard 15 in. by 25 in. If a small square
of the same size is cut from each corner and each side is folded up along
the cuts for form a lidless box. What sizes of squares can be cut from each
corner to produce a box with a volume of 400 cu. in.? What size would produce
the maximum volume.
To find what value for x that V= 400 look at the equation
If we graph this, we get the following picture:
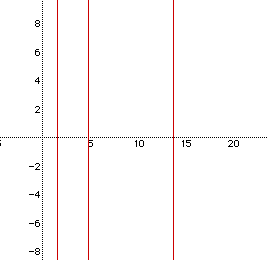
So, we get three possible positive values for x that will satisfy the
equation with the Volume of the given box at 400.
Now if we look at the general equation
we get the following picture.

It appears that the maximum Volume is about 500, and it looks like the
value for x is somewhere around 4. Let's zoom in and see if we can get a
closer estimate.
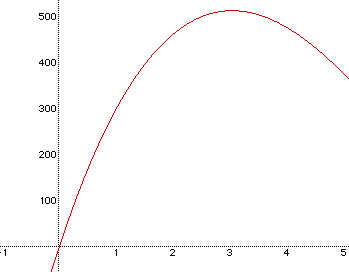
It looks like the value for x where the Volume is the maximum is a little
closer to 3 than 4.
We can look at the derivative of
And we get
If we look at the graph of this, we get the following picture:
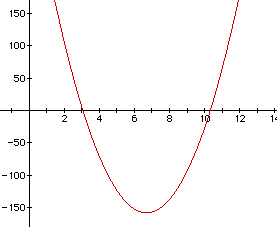
For the equation 0 = 12x-160x+375, you can see that the critical values
for x are about 3 and 10.25, in which x=3 is where the volume is maximized.
If we construct a box similar to the following in GSP
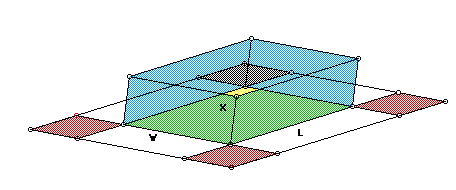
in which we cut out the length x from the sides of a rectangle, it is
easy to see that there is both a maximum and minimum value for x given lengths
L and W for the sides of the rectangle;
(Volume = x(L-2x)(W-2x).)
The following picture demonstrates that there is a maximum value for x(Minimizes
area)
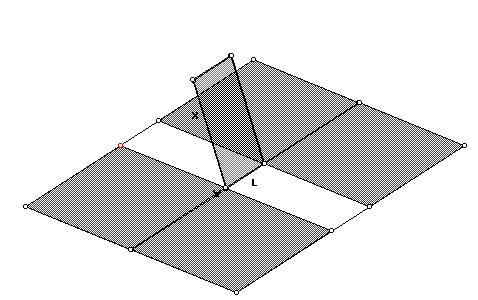
As x approaches the length of either L or W, you no longer have a box,
but a plane (or line).
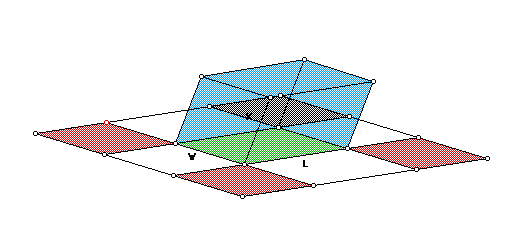
You can compute the lengths of the sides, and measure the volume to see
what is going on with the Volume. For example, in the following picture,
ADAA = L, and ADAQ = W
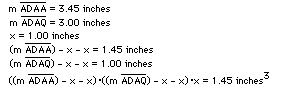
Therefore you can create a box with any given dimensions and by increasing
and decreasing the value for x, see where you maximum Volume might be. You
can also find out what the value for x is given a specific volume and the
lengths of L and W. You just manipulate x until the Volume equals that which
you are looking for.
If in the first column we put the various values for x, second column
is (15-2x), third column is (25-2x), and the last column is (15-2x)(25-2x)x
which is the volume function that we are looking for, then we get the following
information for these values of x.
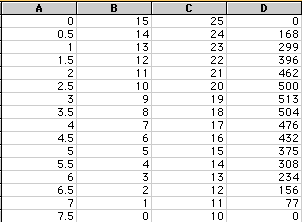
It looks like the maximum value for the volume is where x=3, but we can
fine tune this a little bit to make sure. If we look at the values 2.5 <
X < 3.5 we get the following
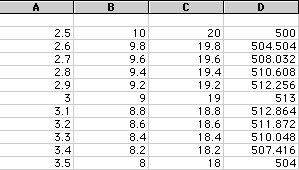
It looks like the Maximum volume is where x=3.
But what if we want the Volume=400. We will look closer at the values 4.5
< X < 5, for one of the values of X.
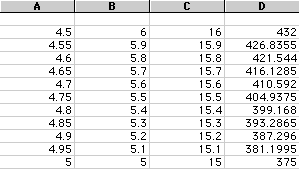
It looks like the value for X is somewhere between 4.75 and 4.8. If we
fine tune this a little more, we get the following.
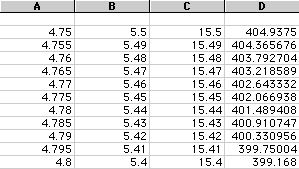
You could keep fine tuning this further to get an exact value, but it
looks like when the volume is 400, one value for x is about 4.79.