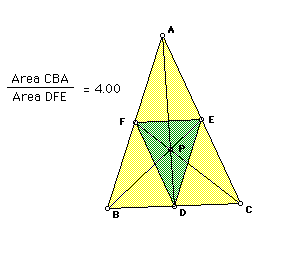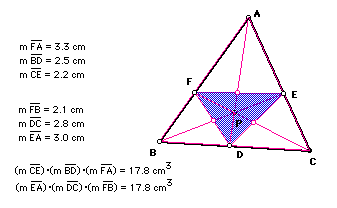

For any point P, it appeas that (AF)(BD)(EC)=(FB)(DC)(EA), but can we
prove that.
In other words we are trying to show that the ratio of the two equals 1.
First we need to construct a line paralled to AD through B, and then another
such paralled ling through C. We get the following picture.
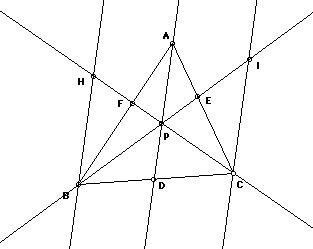
Triangle BDP is similar to Triangle BCI since the corresponding angles
are congruent,
Triangle DPC is similar to Triangle BHC for the same reason.
Triangle HFB is similar to PFA since the alternate interior angles are congruent.
Triangle IEC is similar to PEA for the same reason.
Therefore, we get the following ratios.
Click here to view the GSP file that demonstrates
this.
Click here to view the GSP file that demonstrates
this.
Click here to view the GSP file that demonstrates
this.
If we manipulate the following ratios
we get the following relationship.
Click here to view the GSP file that demonstrates
this.
Using this relationship we get the following
or
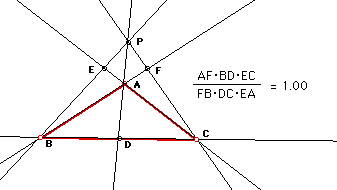
Click here to view the GSP file that demonstrates
this.