Investigation of the Graphs
y = asin(bx+c) and y = acos(bx+c)
For Different Values of a, b, and c
by
Jennifer Roth
First we want to look at a graph of the simplest equations; y = sin(x),(red),
and y=cos(x),(green).
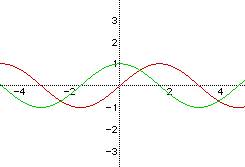
Where do these graphs cross the x and y axis?
Now we want to look at different values of a, b, and c for the equations
y = asin(bx+c) and
y = acos(bx+c).
First we will investigate different graphs for y=asin(bx+c), then we will
investigate different graphs for y=acos(bx+c), and then we will combine
the two.
For each graph, think about where the different graphs crossing the x and
y axis and where are the maximum and mimimum values for x and y. In other
words, what changes are taking place which are caused by varying the values
for a, b, and c?
Example 1
Graph of y=asin(bx+c) changing the value of a, and letting b = 1 and c =
0.
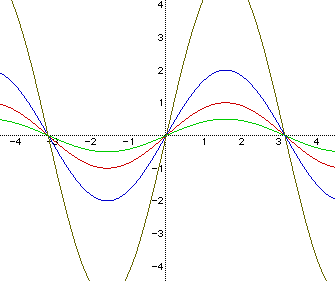
The graphs correspond as follows:
Red: y = sin(x)
Green: y = 1/2sin(x)
Blue: y = 2sin(x)
Brown: y = 5sin(x)
Example 2
Graph of y=asin(bx+c) changing the value of b, and letting a = 1 and c =
0.
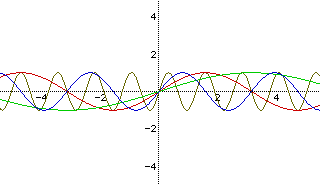
The graphs correspond as follows:
Red: y = sin(x)
Green: y = sin(1/2x)
Blue: y = sin(2x)
Brown: y = sin(5x)
Example 3
Graph of y=asin(bx+c) changing the value of c, and letting a = 1 and b =
1.
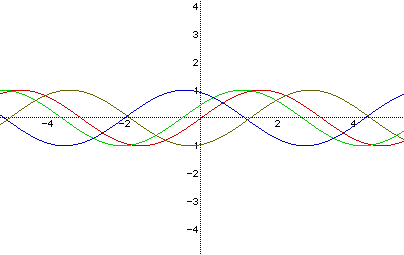
The graphs correspond as follows:
Red: y = sin(x)
Green: y = sin(x + 1/2)
Blue: y = sin(x + 2)
Brown: y = sin(x + 5)
Now we will look at the same graphs for acos(bx+c)
Example 4
Graph of y=acos(bx+c) changing the value of a, and letting b = 1 and c =
0.
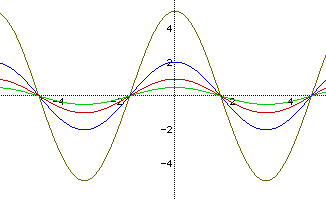
The graphs correspond as follows:
Red: y = cos(x)
Green: y = 1/2cos(x)
Blue: y = 2cos(x)
Brown: y = 5cos(x)
Example 5
Graph of y=acos(bx+c) changing the value of b, and letting a = 1 and c =
0.
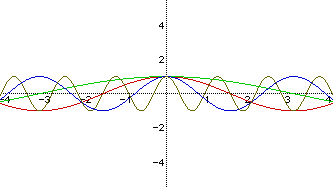
The graphs correspond as follows:
Red: y = cos(x)
Green: y = cos(1/2x)
Blue: y = cos(2x)
Brown: y = cos(5x)
Example 6
Graph of y=acos(bx+c) changing the value of c, and letting a = 1 and b =
1.
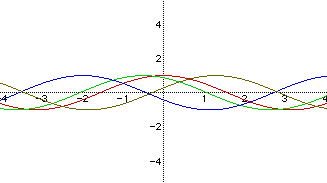
The graphs correspond as follows:
Red: y = cos(x)
Green: y = cos(x + 1/2)
Blue: y = cos(x + 2)
Brown: y = cos(x + 5)
Now we will combine the graphs of asin(bx+c) and acos(bx+c). First we
will combine the graphs for both , varying a, then b, and then c.
Example 7
Graphs of y = asin(x) and y = acos(x)
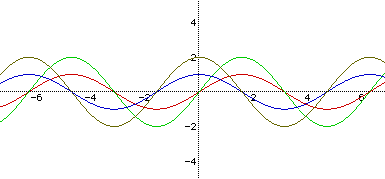
The graphs correspond as follows:
Red: y = sin(x)
Green: y = 2sin(x)
Blue: y = cos(x)
Brown: y = 2cos(x)
Example 8
Graphs of y = sin(bx) and y = cos(bx)
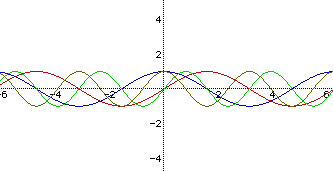
The graphs correspond as follows:
Red: y = sin(x)
Green: y = sin(2x)
Blue: y = cos(x)
Brown: y = cos(2x)
Example 9
Graphs of y = sin(x + c) and y = cos(x + c)
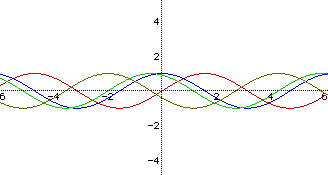
The graphs correspond as follows:
Red: y = sin(x)
Green: y = sin(x+2)
Blue: y = cos(x)
Brown: y = cos(x+2)
Example 10
It might be interesting to look at all the graphs combined.
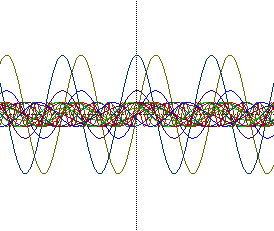
What conclusions can be made about the affect of different values of
a, b, and c on the graphs of y=asin(bx+c) and y=acos(bx+c)?
Back to Jennifer's Home Page











