These are some records and observations made during
EMT 668 Assignment 1
Activity 2
Activity 2.
Make up linear function f(x) and g(x). Explore, with different pairs
of f(x) and g(x) the graphs for
i. h(x) = f(x) + g(x)
ii. h(x) = f(x) . g(x)
iii. h(x) = f(x) / g(x)
iv. h(x) = f(g(x))
Summarize and illustrate.
I will approach this from a purely exploratory perspective - that is
I will attempt to explore the properties of teh four cases using Algebra
Expressor as a tool of exploration. The observations I will make will be
based on the information gleaned from the graphs drawn by Algebra Expressor
rather than on any algebraic manipulations. I justify this as follows: I
believe that I am capable of the algebraic manipulations. However, I am
trying to make a case for the use of the computer as a tool of investigation
and would like to demonstrate its power by using it as such!
In this activity I will explore all four cases at a time. For each case
I will report the values of the variables a,b,c,d as in:
f(x) = ax + b
g(x) = cx + d
Let us begin with the case where f(x) and g(x) have the same co-efficients
of x but different constants :

fig 1: a = c = 1, b = 2, c = -2
Let us change the co-efficients of x to be opposite in sign and see what
happens:
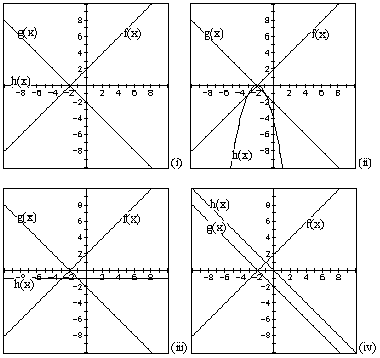
fig 2: a = 1, b = 2, c = -1, d = -2
This time let us explore what happens when the coefficients of x are
different both in magnitude and opposite in sign:
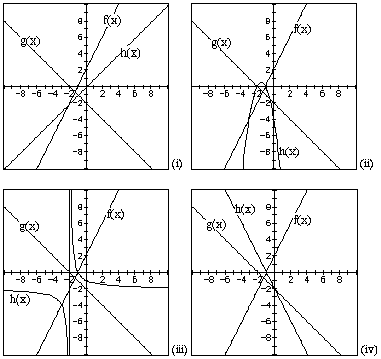
fig 3: a = 2, b = 2, c = -1, d = -2
Next we explore the case where the co-efficient of x is opposite in sign
but similar in magnitude and the two constants are the same:

fig 4: a = 1, b = 2, c = -1, d = 2
Finally let us consider the case where the coefficients are both opposite
in sign and magnitude while the constants are the same:
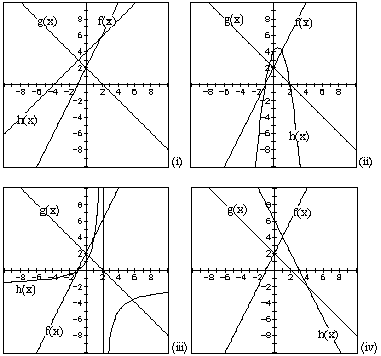
fig 5: a = 2, b = 2, c = -1, d = 2
Without considering greater differences in the actual numbers used we
are in a position to consider soem trends and make some conjectures. To
begin with let us summarise what we have seen:
SUM OF FUNCTIONS: h(x) = f(x) + g(x)
h(x) will be a straight line, both the y intercept and gradient are the
sum of the y intercepts and gradients of f(x) and g(x). A horizontal line
is possible if the gradients of f(x) and g(x) are equal and opposite in
sign. No vertical lines are possible
PRODUCT OF FUNCTIONS: h(x) = f(x) + g(x)
As can be expected (linear x linear = 2nd degree equation) the result is
a parabola. The shape of the parabola is effected by:
"arms-up parabola" when gradients of f(x) and g(x) have the same
sign,
"arms-down parabola" when gradients of f(x) and g(x) are opposite
in sign,
x-intercepts of the parabola x1 and x2 are the x intecepts of f(x) and g(x),
the gradients of the linear functions will determine the number of cuts
of the original linear functions with the parabola - THIS IS THE SUBJECT
OF ACTIVITY THREE
QUOTIENT OF FUNCTION: h(x) = f(x) / g(x)
h(x) is an interesting function. There are two different shapes adopted
by h(x)
(i) h(x) is a straight line parallel to the xaxis, and
(ii) h(x) is a rectangular hyperbola with asymptotes paralel to the x and
y axis.
based on the cases explored so far it is too early to conjecture
(i) when we will get a straight line rather than a hyperbola, and
(ii) when the hyperbola will be in the "1st and 3rd quadrants"
vs "2nd and 4th quadrants"
some further exploration will reveal answers to these questions.........
FUNCTION OF A FUNCTION: h(x) = f ( g (x) )
This is not as interesting as the previous cases - the result is a straight
line (linear function) - which is quite easy to understand based on the
structure of h(x). What remains is to prepare a conjecture on how the coefficients
of x in f(x) and g(x) determine the gradient of h(x).
To go to activity
3 (WRITE UP 1) click here.
To return to Aarnout's EMT 668 page
click here.





