This is one of my favourites. I use this example to introduce Calculus
to students at my school, but rather than using the technology (only because
it is not available yet) the students make the boxes from cardboard.
There are three tools that we will use - each is quite different in terms
of what it can do and yet none of the three will provide the answer - we
cannot pose the problem to any of the three tools and get a "printout"
that says cut off so many inches.
An important starting point is to understand the problem - I think that
GSP is the most powerful tool in this regard.
Looking at the problem from the perspective of GSP.
Using the animate facility we are able illustrate the manufacture of
a box as different sizes of square are cut out of the sheet of cardboard.
Begining with a rectangular sheet:

We can cut squares (yellow) from the corners and fold up the sides to
make a box. At the same time we can have GSP meausre the various dimensions
of the box and determine the volume for us.

It is quite obvious that there is a limit to the size of the squares
that we can cut out:

Using the animate facility we can let the box "grow" before
our eyes (click here to enjoy that experience)
- in fact we can also drag the critical point on the construction and control
the "growth" of the box. Using the tabulate function we can record
the dimensions at various moments in the life-cycle of the box.
GSP is able to provide us with a feeling of the dimensions for which the
box will have the required volumes but is unable to give us the exact measures
as a result of the limitations of the software.
Looking at the problem from the perspective of Excel.
To be able to explore the problem using a spreadsheet we need some formulas
- I trust that the reader is happy, based either on their knowledge of the
problem or on their understanding of the problem to accept the following
formulae (if not please revisit the diagrams above or the GSP animation
to ensure that you are happy with them):
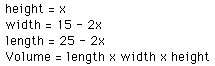
If we place the formulas into various collumns and let x vary between
0 and 7.5 inches (check that you are happy with this dimension) we could
generate a table (and from the table a graph) something like this:
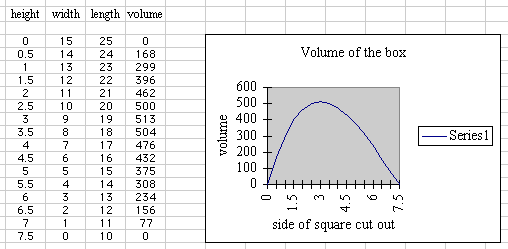
As with the GSP experience this gives us a feeling for the values requested
- that is for a volume of 400 cu. in. we need to either cut of a square
with dimension 1.5 < x < 2 or a square with dimension 4.5 < x <
5 and for a maximum volume teh square should have dimension 2.5 < x <
3.5. Certainly you may argue that using the graph we could narrow the range
of x values slightly but that is of little consequence.
We can now return to Excel and perform exactly the same operation but in
the three small areas noted above and for very much smaller steps in height:
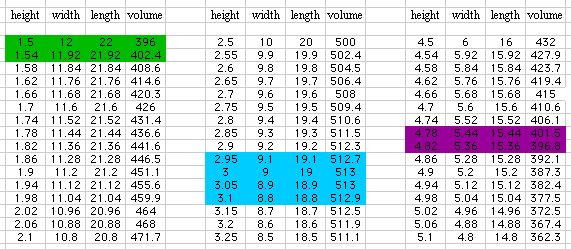
Returning yet again we can refine the values still further:
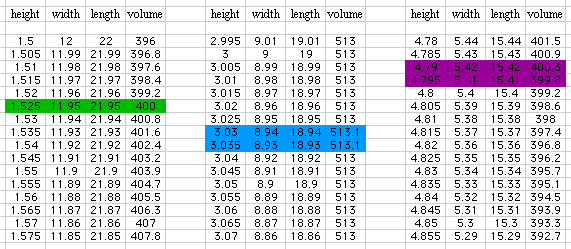
So you can continue reaching degrees of accuracy that exceed your ability
to cut the square that accurately.
Loking at the problem using Algebra Xpresser
We will again use the formulae noted earlier and draw the graph:

Notice how this graph gives alot more information than the previous examples
did - namely there is a suggestion that a negative volume is possible for
values of x < 0 or 7.5 < x < 12.5 (blue region)? Furthermore an
almost infinite volume is possible if we cut of squares with sides greater
than 12.5?? I believe that this is a valuable opportunity for introducing
concepts such as domain and range.
How do we proceed from here in a pre-calculus class we may use the zoom
facility to find values of x for which the volume is a max and solve the
equation x(15 - 2x)(25 - 2x) = 400 to answer the other question. In a class
familiar with calculus we could solve for zero in the derivative to tell
us the value of the side of the square to be cut off:
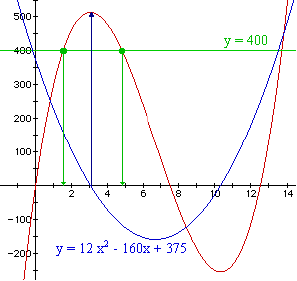
By zooming in we can "read" the critical values of the graph:

Conclusion
I hope in answering this question to have demonstrated that the three tools
discussed are very powerful in helping students understand and explore this
very interesting problem.