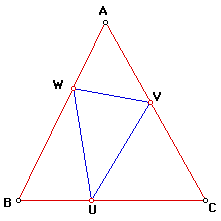

In this proof (by Coxeter) consider any triangle UVW in triangle ABC and reflect UW and UV in AB and AC respectively.
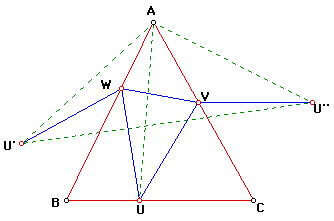
Now: UV + VW + WU = U''V + VW + U'V the path from U' to U'', such a path is minimum when it is a straight line :
Hence for all the inscribed triangles with vertex U on BC the one with
smallest perimeter occurs when V and W lie on the straight line U'U'' click here for a GSP animation.
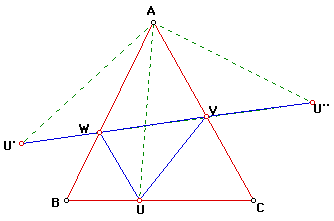
By this technique we can find the triangle of minimum circumference for
each choice of U. The problem that remains is to find the position of U
for which the U'U'' is a minimum. Now AU' and AU'' are both equal to AU
(by our construction) hence triangle AU'U'' is isosceles and its base will
be a minimum when its equal sides are a minimum - ie when AU is a minimum
- when AU is the shortest possible distance. Clearly this occurs when AU
is the altitude from A to BC. Since we could easily have started with B
or C rather than A, it follows that CW and BV are altitudes also.
