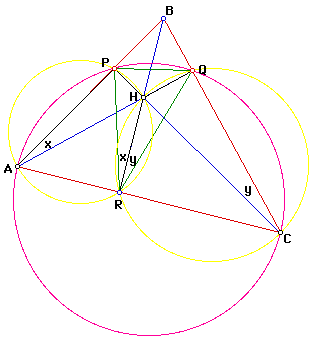

Quadrilateral APHR is cyclic since opposite angles APH and ARH are supplementary
(in fact they are 90deg each).
Hence angle PAH = angle PRH.
Similarly angle QRH = angle QCH.
Quadrilateral APQC is cyclic since AC subtends angle APC = angle AQC (both
= 90 deg).
It follows that angle PAQ = angle PCQ and by the earlier discussion that
angle PRH = angle QRH. ie HR bisects angle PRQ.
Similarly HP bisects angle RPQ and HQ bisects angle PQR and H is the incenter
of triangle PQR!