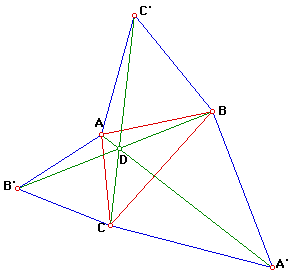

Rather than limit the investigation to the case of isosceles triangles
whose height is equal to their base let us explore the full range of isosceles
triangles - that is we will consider isosceles triangles whose base angles
are equal (similar isosceles triangles).
Some reflection will suggest that we are dealing with a general case of
the other tasks discussed:
Consider:
1. When the base angles are 60deg the exterior triangles are equilateral
and we have Task C and the point of concurrency
of the lines AA', BB' and CC' is the Fermat point
of the triangle.
2. When the exterior triangles have base angles of 30deg we have Task A,
when the base angles are 45deg we have Task B and when the base angles are
-60deg (or equilateral triangles built toward the inside) we have Task E.
3. When the base angles are 0deg - it is quite obvious that the point of
concurrency of the lines AA', BB' and CC' is the centroid

It seems reasonable to expect that the position of D will be determined
by the base angle of the externally constructed isosceles triangle. We therefore
expect a locus for D that will incorporate the five points of concurrency
shown. The figure below illustrates the locus of D as the base angle of
the isosceles triangles vary from 90deg to -90deg.

Our predictions are confirmed. What about the other points that we are
familiar with: Orthocenter (H), Circumcenter
(C), Incenter (I) and center of the nine
point circle (N)?

It seems as though the Orthocenter is indeed a member of the locus while
the Circumcenter (C), Incenter (I) and center of the nine point circle (N)
do not lie on the locus. As with the Centroid it makes sense that the Orthocenter
(H) should lie on the the locus - as the base angle tends toward 90deg so
the intersection of the lines AA', BB' and CC' tend toward the Orthocenter.
For a GSP sketch that draws the locus of point D click
here.
More than answering questions our discovery of a locus that looks like a
hyperbola begs further questions, for example:
How does the shape of triangle ABC influence the shape of the locus? Let
us consider the following cases (in the obtuse-angled cases we will make
the obtuse angle greater than 120deg so that the fermat point is outside
the triangle) click on the case to view a sketch:
1. ABC is an equilateral triangle.
2. ABC is an acute-angled isosceles triangle.
3. ABC is a right-angled isosceles triangle.
4. ABC is an obtuse-angled isosceles triangle.
5. ABC is an acute-angled scalene triangle.
6. ABC is a right-angled scalene triangle.
7. ABC is an obtuse-angled scalene triangle.
Summary of observations made:
1. If ABC is an equilateral triangle the locus is a point!
2. In all cases where triangle ABC is isosceles the locus is a a straight
line passing through the vertical angle and bisecting the opposite side.
3. In all cases where the triangle ABC is scalene the locus is a hyperbola
one arm of which passes though the two vertices at the largest and smallest
angles of triangle ABC and the other arm touching the triangle ABC at the
vertex that is at the smallest angle.
4. For each of our points there is a critical for which that point will
coincide with a vertex of the triangle.