The Lidless Box Problem
Using Excel

by

Helene Chidsey and Lou Ann Lovin

Here is the problem again for reference:
Given a rectangular sheet of cardboard 15 in. by 25 in., what size square should be cut from each corner to produce a box with a volume of 400 cu. in.? What size square would produce the maximum volume? (The square cut from each corner needs to be the same size since we want to fold each side up along the cuts to form a lidless box.)

Excel Investigation

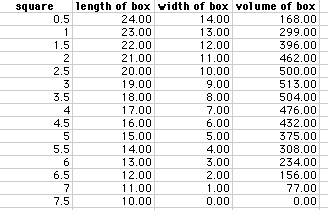
In the first column, we entered the size of the square to be cut from each corner [x]. In the second and third columns, we calculated the length [25-2x] and width of the box [15-2x], respectively, and in the fourth column, the volume of the box [x(25-2x)(15-2x)]. In the following table the square increases in size by 0.5 in. each time.

The maximum volume is 513 cu. in., at x=3 in. To produce a box of 400 cu. in., x is either between 1.5 and 2 in. or between 4.5 and 5 in.

In order to calculate more accurately, we can use a smaller increment for the size of the square, x. Thus below we started at x = 1.5 in. and increase in steps of 0.05 in.


.
.
.

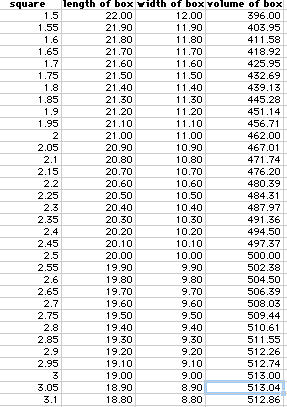
Now the maximum volume is 513.04 cu. in., at x=3.05 in. Also, to construct a box of 400 cu. in., we need x either between 1.5 and 1.55 in. or between 4.75 and 4.8 in.

Again, we can use a smaller increment to improve the accuracy. Below we started at 1.521 in. and increase in steps of 0.0003 in.


.
.
.


.
.
.

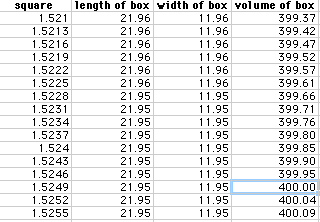
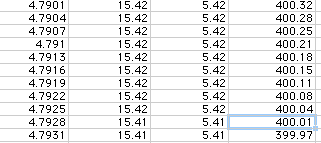
Now we see that the maximum volume is 513.05 cu. in., at x = 3.0461 in., and at x = 1.5249 in. or 4.7928 in. the volume of the box is approximately 400 cu. in.

Thus, we could continue to decrease the size of the increment to improve the accurracy.

Return to Final Page