An Exploration of Linear Functions

by

Helene Chidsey and Lou Ann Lovin

In this exploration we investigate different pairs of linear functions, f(x) and g(x), using addition, multiplication, division and composition to obtain a new function h(x). We chose to consider the following pairs of functions throughout:

f(x)= (x+1) , g(x)= (2x+3);

f(x)= - (x+1), g(x)= (2x+3);

f(x)= (x+1), g(x)= - (2x+3); and

f(x)= - (x+1), g(x)= -(2x+3).

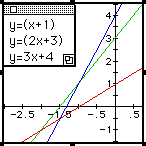
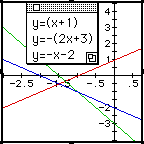
In this way we can systematically view the effects of changing the operation as well as the effects of negative functions.


I

In part one we added f(x) and g(x) to obtain a new function h(x). Notice throughout part I that

f(x) is the red line,
g(x) is the green line, and
h(x) is the blue line.






These graphs show us that the sum of two linear functions is a linear function. Notice too, that the slopes and y-intercepts of h(x) are simply the sum of the slopes and y-intercepts respectively of f(x) and g(x). (The reader may notice that this is similar to vector addition and vaguely similar to multiplication of complex numbers, where the angles are added!) Thus when just f(x) or g(x) is negative, h(x) is more of a "mix" of the two, while it is a more obvious addition of the two in the first and fourth frames. One can also see that the negative of a linear function is a reflection in the line through the x-intercept of that function. In other words in figures 1 and 2 the red lines [f(x) and -f(x)] are a reflection about the line x=-1.

II

In part II we multiplied f(x) and g(x) to obtain h(x). [Throughout the rest of this investigation we assume the reader can recognize the linear graphs f(x) and g(x). If not refer back to the colored graphs in part I!]



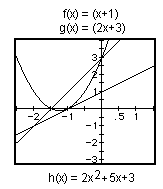
We see clearly from the above figures that the product of two linear functions is a quadratic function. It is also readily apparent either by viewing the graphs or doing the algebra, that when f(x) and g(x) are both negative we obtain the same graph as we when they are both positive since,
-1(-1)=1. Similarly, regardless of which function is negative [f(x) or g(x)], h(x) is the same. Notice also that in the bottom figures h(x) is the negative of h(x) in the top figures. Thus the parabolas are "upside down", or reflected about the x-axis.

III

In part III h(x) = f(x)/g(x).


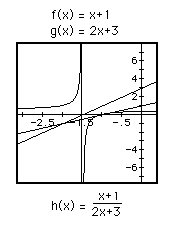
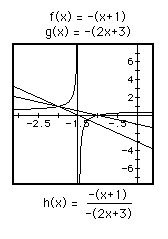
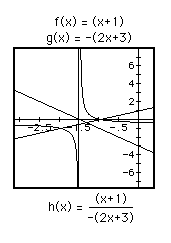
So we see that division of two linear functions results in a hyperbola. The equations corresponding to the top figures are in fact the same. Likewise the equations corresponding to the bottom figures are equal. Furthermore, the bottom equation is simply the negative of the top, resulting in a reflection about the x-axis.

IV

In this last section we used compostion of f(x) and g(x) to obtain h(x). [h(x) = f(g(x))].
For the reader's convenience we simplified h(x). As an exercise the reader may choose to verify that these are correct!


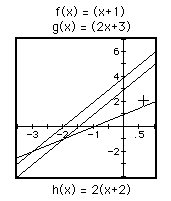
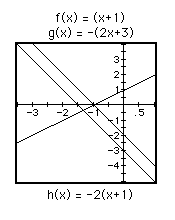
Again from these pictures, it is clear that composition of two linear functions produces a linear function. Since we are composing f of g of x, we notice that taking the negative of f(x) results directly in the negative of h(x) [compare the top figures as well as the bottom figures]. On the other hand, the negative of g(x) totally changes h(x) [Compare the left figures, top and bottom. Now compare the right figures, top and bottom.].


A Note to the Reader:

We chose this particular assignment because we felt that it would help students to see what happens when combining functions with various operations. We suggest that you allow students to make conjectures about the result of an operation on two linear functions. Then they can use technology to test their hypotheses. In particular, students often have a hard time grasping the concept of composition and this investigation demonstrates the result of composition of linear functions.

As an extension, students could do a similiar investigation with quadratic as well as cubic equations.

We feel that our best work is demonstrated in our write ups (1-5), on which we spent the majority of the quarter. It can however be noted that we spent a considerable amount of time (MANY, MANY, MANY HOURS!!!!) on the final as well!

Return to Final Page.