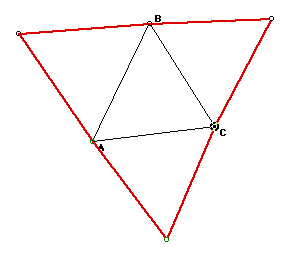

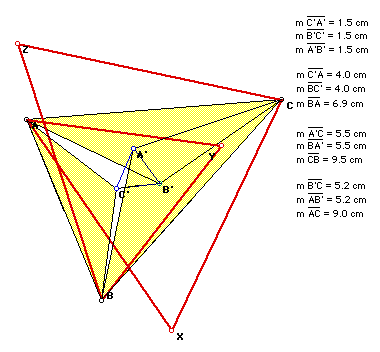
The three red triangles are thus all constructed to be equilateral. Now
we will locate the centroid of each triangle and label them A', B', and
C' (Where A' is opposite A, B' is opposite B, and C' is opposite C). And
then we constuct lines AA', BB', CC'.
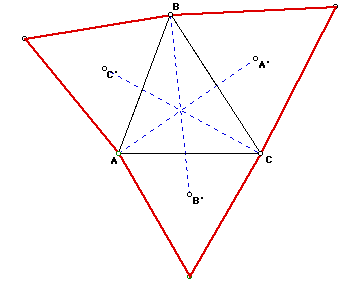
As points A, B, and C are translated, the lines AA', BB', and CC' remain
concurrent. Click here to view the GSP file
that demonstrates this.
This point of concurrency, say P, is not the orhocenter, centroid, incenter,
or circumcenter of "any" triangle ABC. If we find these four points
for ABC we can demonstrate that none of these points is the same as point
P. But, there are also many other things going on in this construction.

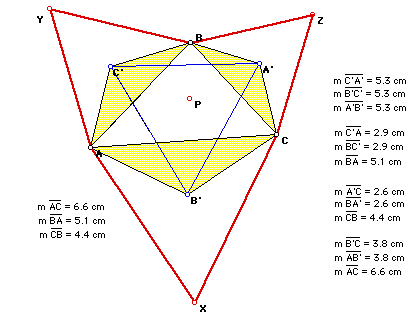
The simplest case is when the given triangle ABC is an equilateral triangle
(As shown above). In this case the orthocenter, centoid, incenter, and circumcenter
are all equal to P (And this is only true for this case). If we construct
these four points they will all overlay P. The larger triangle created XYZ
is also an equilateral triangle.
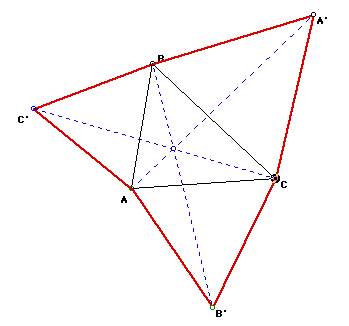
The Triangles ABC', ACB', and CBA' are all iscoceles, and the triangle A'B'C'
is equilateral. These two things are also true, however when ABC is not
equilateral. (See the following picture)
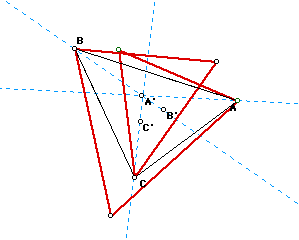
If we were to translate A, B, and C, then ABC', BCA', and ACB' remain
iscoceles, and A'B'C' remains equilateral. Click here
to view the GSP file that shows this animation.
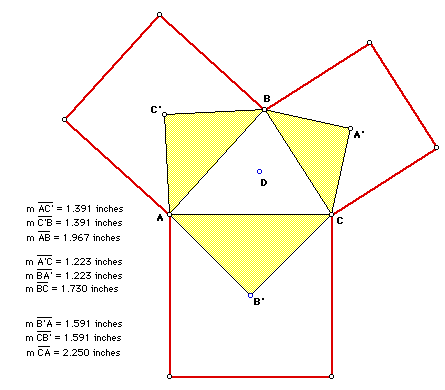
We can also do a similar construction using a square.
It also appears that our other conclusion hold true for this construction
also.

The point D is the point of concurrency for the three lines AA', BB',
and CC'. Click here to view the GSP file that demonstrates
this.
The triangle AC'B, CA'B, and AB'C are all isosceles triangles.
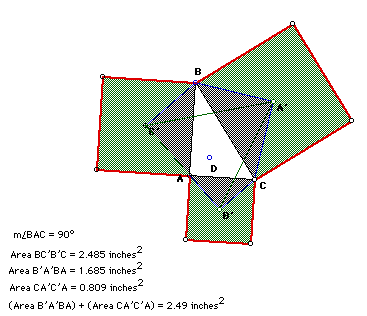
But unlike the constuction with the equilateral triangles, when we construct
the squares, the Triangle A'B'C' is not equilateral. Click here
to view the GSP file that demonstrates this.
If the given triangle is a right triangle, then we will get a representation
of the Pythagorean Theorem as follows.
Further investigations might include other regular figures constructed
on the sides of a triangle, or using other regular figures as the base.
For example, what if the center figure is a square and you draw triangles
on the sides.