

What happens if we change k? If we let k = 4, leaving a and b both equal
to 1, we get the following graph.
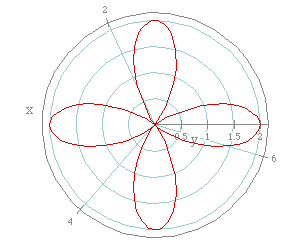
Now there are 4 leaves, and remember what the value for k was!
One more graph with a and b both at 1 and a different value for k might
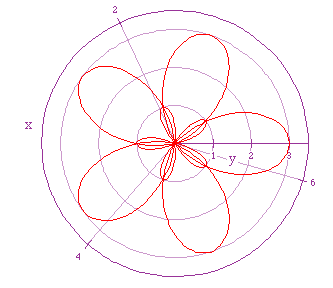
help us make some conclusions. If w let k = 6, we get the following graph.

Now there are 6 leaves, and we set k = 6. It appears that the number
of leaves of the rose is determined by k, but we need to do some further
investigation letting a = b with different values for a.
If we let a = 2 = b, and let k = 1, we get the following graph.

Compare this to our first graph in which we set a = 1 =1 and let k =
1.
Now we will vary k, and let a = 2 = b. In the following graph we set k =
6.
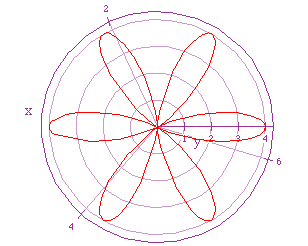
This graph looks like the graph in which we set a = 1 = b, and let k
= 6. So, it "appears" that when a and b are equal, and k is an
integer we get a k-leaf rose.
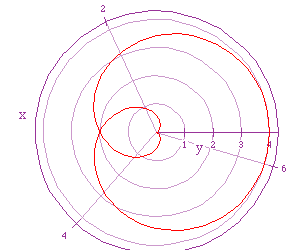
How does this compare to our original graph in which a = 1 = b, and k
= 1.
If we let a = 2 = b, and k = 5/2, we get the following graph.
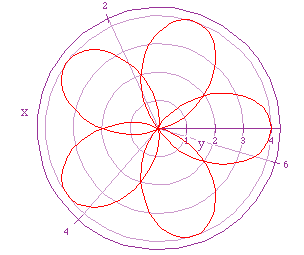
We have a 5-leaf rose, but the leaves overlap to get two sets of 5-leaf
roses. So, it appears we will get a m sets of n-leaf roses for k = n/m.
Lets view more graphs to see if this holds true.
If we let a = 2 = b, and k = 1/3, we get the following graph.

And, if we let a = 2 = b, and k = 4/3 we get the following graph.

It appears that we are getting m sets of n-leaf roses for k=4/3, but
what if we vary the values for a = b.
If we let a = 1/2 = b, and let k = 4/3, then we get the following graph.
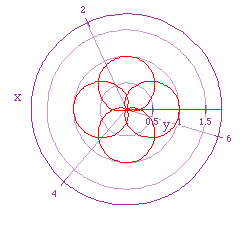
It appears the same thing is going on here.
What conclusions can be made?
How does this compare to our other graph's. Let's do some more graphs
and see what conclusions we can draw.
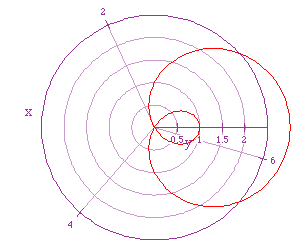
If we again let a =1, b = 2, but let k = 6, we get the following graph.

So it appears we are getting 2 sets of k-leaf roses in this case. So,
where is the 2 soming from. Let's vary a and b, and see if there could be
some relation between their values and the number of sets.
If we Let a = 1, b= 3, and let k = 6, we get the following graph.

It appears we are still getting 2 sets of k-leaf roses. If we do further
graphs for different values of a and b as long as a < b, and k is an
integer value we will get 2 sets of k-leaf roses.
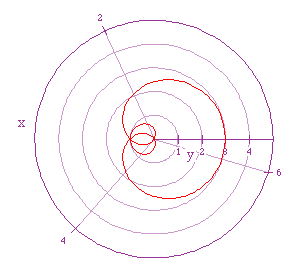
If we let a = 1, b = 2, and k = 5/2 we get the following graph.
So, what is going on with these graph's that is different from the other
sets of graphs?
It might be easier to see if we look at some different values for k.
If we let a = 1, b = 2, and k = 1/3 we get the following graph.

If we let a = 1, b = 2, and k = 4/3, we get the following graph
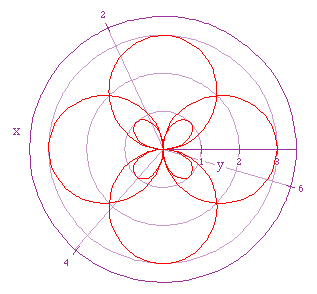
What conclusions can we draw? How many sets of roses do we have, and
how many leaves does each rose have?
Now we will look at graphs with b < a , and k set equal to a non-integer
value.
If we let a = 2, b = 1, and k = 1 we get the following graph
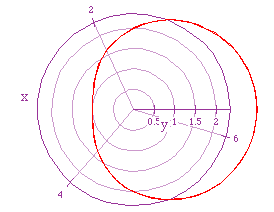
If we let a = 2, b = 1, and k = 1/2, we get the following graph.
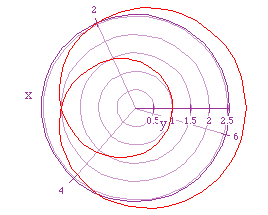
Again we will let a = 2, and b = 1. If we let k = 5/2 we get the following
graph.

Look at the other graphs in which k = 5/2. What is going on here that
is different?
Let's look at some more values for k and see if we can make any conclusions.
If we again let a = 2, and b = 1, and let k = 1/3, then we get the following
graph.

And, in the following graph k = 4/3

Make comparisons with this graph and the other graphs. What conclusions
can be made for:
1) a = b, k integer value
2) a = b, other values for k
3) a < b, k integer value
4) a < b, other values for k
5) b < a, k integer value
6) b < a, other values for k
What kind of general conclusions can be made?