
Department of Mathematics Education
J. Wilson, EMT 669

1. Given a triangle ABC, find a point D such that line segments AD, BD, and CD trisect the area of the triangle into three regions with equal areas.
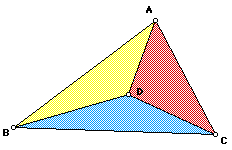
Define D and prove that the triangle is divided into three regions of equal area. Show a construction for finding D.
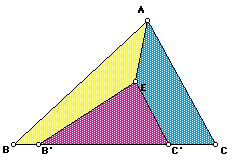
Show a construction and prove that it divides the triangle into three regions of equal area. Are there restrictions on the location of E within or on the triangle?
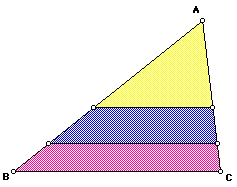
Prove that the construction divides the triangle into three regions of
equal area.