
Department of Mathematics Education
EMT 669, Jim Wilson
Triangle Construction Problems
In these problems, information is given about a triangle to identify physical
attributes. The problem is to describe ruler and compass constructions of
the triangle from the given attributes. For consistent notation adapted
to this environment I use the following:
The angles at vertices A, B, C: A, B, C
The sides of the triangle opposite vertices A, B, C: a, b, c.
The medians: m(a), m(b), m(c)
The altitudes: h(a), h(b), h(c)
The segments along an angle bisector to the opposite side: d(a), d(b),
d(c)
The radius of the circumcircle: R
The radius of the incircle: r
The radii of the excircles: r(a), r(b), r(c)
The notation m(a), etc., is usually written with a subscript and I will
do so in the sketches. The notation: b+c will mean "given a
line segment equal in lenght to the sum of the lengths of sides b
and c.
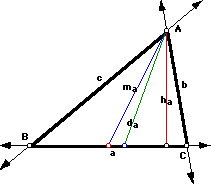
1. Triangle, given two sides and the median to the third side.
b, c, m(a)
One Solution (In Microsoft Word)
A GSP Sketch
A GSP Script
2. Triangle,
given two angles and the perimeter
A, B, a+b+c
3 . Triangle, given the three medians
m(a), m(b), m(c)
4. Triangle, given two sides and the angle opposite one of the sides
a,b,A
5. Triangle, given two sides and the altitude to the third
a,c, h(b)
6. Triangle, given a side, the median to that side, and another median
b,m(b), m(a)
7. Triangle, given a side and the angle subtending (opposite of) that
side, and a segment equal to the sum of the other two sides.
a, b+c, A
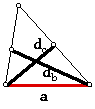
8. Triangle, given a side and the angle bisecting segments to the sides
opposite each endpoint of the given segment.
a, d(b), d(c)
9. Triangle, given the perimeter, an angle, and the altitude from that
angle.
a+b+c, A, h(a)
10. Triangle, given a side, an angle adjacent to the side, and a segment
equal to the sum of the other two sides.
a, B, b+c
11.
b+c, B, h(c)
12.
b+c, C, h(b)
13
b+c, A, B
14.
b+c, a, h(b)



