Pythagorean Theorem
by:
Heather Bridges
The following information is an outlined attempt as to how to present the
Pythagorean Theorem to high school students. There are several proofs that
have been used to explain why this theorem is true but, the best way to
illustrate it to the students may be through their own hands on exploration.
Step 1: Create several different sizes of right triangles all of whose
sides can be squared using one piece of construction paper. Then distribute
these triangles to the students after they have been assigned to groups.
The students have two assignments at this point:
1. The students need to create 3 squares using the construction paper provided
in three different colors that have the side lengths of the 3 sides of their
triangles. (Note: Have the students use the side of the triangle to measure
for their squares. It is not necessary to measure exact length using a
ruler. The students hopefully at this point are familiar with the areas
of squares and so forth.)
The teacher should check to make sure each group has completed assignment
#1 before proceeding on to the next assignment.
2. The students should then use their largest triangle as the game board
and the two smaller triangles as their playing pieces in a matter of words.
What the students need to do is see if they can cut and rearrange the smaller
triangles on top of the larger to equal the same amount of area. (Note:
remind the students to be very careful when cutting to not lose area.)
Hopefully, every group in the class will discover that the area of the big
triangle is equal to the area of the sum of the two smaller triangles regardless
of the size of the right triangle.
Alternative: It may even be helpful for a couple of the groups in the room
to experiment with an acute or obtuse triangle to illustrate that this method
works for only right triangles.
Step 2: Bring the students back together for a classroom discussion. See
if anyone can interpret what the class together has just discovered given
the following.

The students should see from the background dealing with the area of
squares that the squares they created using the given lengths a, b, and
c have the following areas.


And because of the class discoveries the students found that the area of
the two smaller squares equals the area of the largest. Therefore they
have single handedly discovered
The Pythagorean Theorem 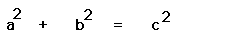
Step 3: Reinforce the students understanding by having them to go to the
computers and basically repeat what they just did using The Geometer's Sketchpad.
Starting with constructing a right triangle properly. Then constructing
the squares on each side of the right triangle. The students should then
measure the areas of the squares to check to see if their previous assumptions
still hold true with exact measurements. The students could then drag the
vertices of their triangle to see if it works for any size right triangle.
Extension: Have the students to use the side lengths to construct other
figures using sketches to see if the areas of the three figures still behave
in the same manner. This exercise might provide some more room for creativity
and student interest.
Return to Great Theorems
Page.





![]()