where
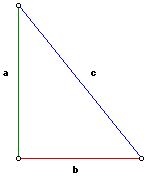
This theorem can be proven by using a right triangle and form squares
around each leg. The area of square a + the area of square b should equal
the area of square c.
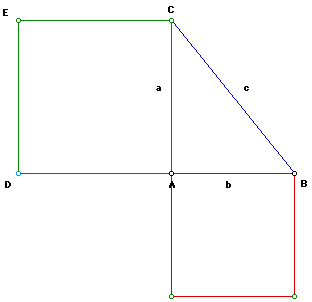
The first step in constructing square a is to extend leg b and construct
a parallel line through point C and parallel to line AB.
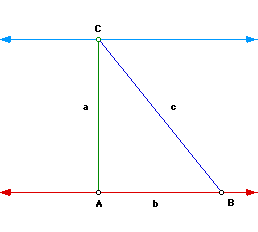
Now using point A as the center and segment a as the radius construct a circle. Where the circle and line AB meet label it D. Next use point C and the same radius a and construct a circle. Label the point E where the circle and the line C meet.
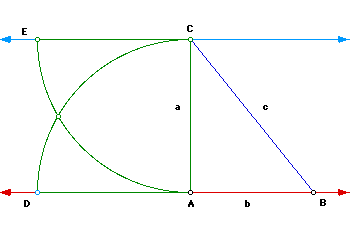
Next connect ACED and this forms your square a.
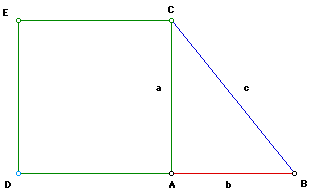
You can do the same consturction for the other two squares. Square b should look like this:
The finished 3 squares should look like this:
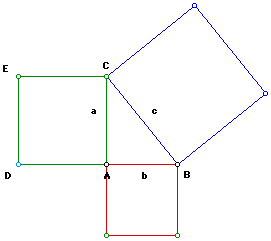
Now let's explore the areas of the squares.
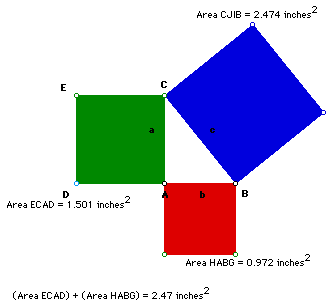
As you can see the red square plus the green square equals the blue square.