Open Geometer's Sketchpad,and open a new scetch and a new script. Click
record on the script before you begin to construct on the sketch. Follow
the directions below to create a hat fractal.
1. Construct two points and the segment between them. Mark the left point
as the center and dilate the right point by a factor of 2/3. Then mark the
right point as the center and dilate the left point by a factor of 2/3.
(To mark a point as a center, double-click on it. The dilate tool is found
under the transform menu) This action trisects the segment.
2. Next, rotate the second point (from the left) -90 degrees about the
third point, and rotate the third point 90 degrees about the second point.
(using the rotate function under the transform menu, making sure to mark
the center of rotation)
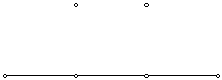
3. Now, hide the original segment, and construct segments between the points
as pictured below.

4. Beginning on the left, highlight the first and second points (holding
down the shift key). Click on your script that is recording the construction,
and click "loop." Go back to your scetch, and highlight the second
and third points and again, loop. Do the same for each set of consecutive
points (3rd and 4th, 4th and 5th, and 5th and 6th). Then hide all the points
except the original endpoints, and finally click "stop" on your
script. Now you have recorded a recursive script that will create your fractal.
5. To play your script, open a new scetch, and construct two points. Highlight
them both and click "fast" on your script. It will ask you how
many recursions you would like. Recursions take a lot of memory, so don't
choose too many (your computer will tell you if you have). The following
picture was made with 3 recursions:
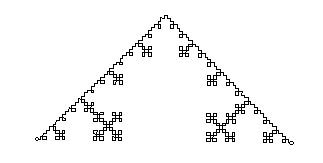
Using the same method of recording a script and recursing, try to create
a script to generate the following fractal, called the Koch curve.

Now, using the same script, try to generate a Koch snowflake:

Now, create your own fractal, and scripts to construct it. Write directions
as to how to create a script to construct your fractal, and give the directions
to a friend and see if they're able to make your fractal.
List your instructions below, and print a picture of your fractal and attatch
it to this paper.