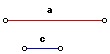
Show that there exists a segment of length b that can lead to the following construction.
Part of the construction is to show that there exists a line through the center of both the circles
of radius a and b and is tangent to the circle of radius c. All three circles must be tangent to the
base line, then circles with radii a and c must be tangent as well as the circles of radii b and c.



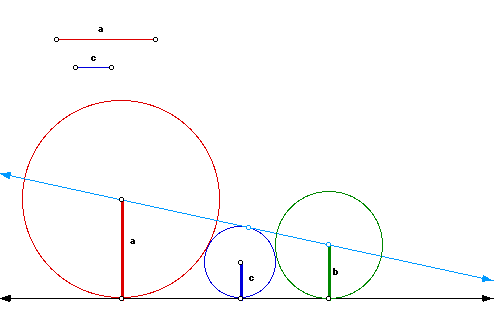
To this extent we found at least two different constructions.

The first of which involved starting from the radius c and working outward from there.






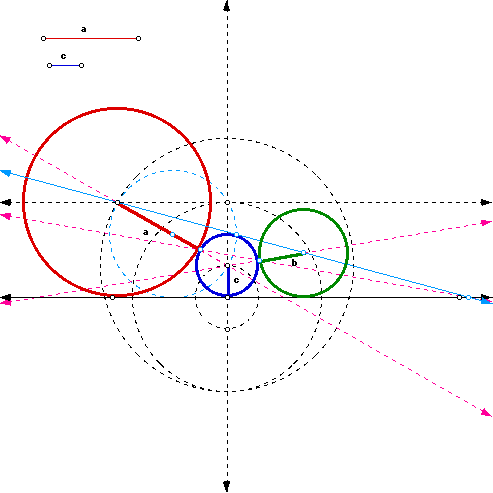
click here for the first GSP construction.


The second construction we started with the radius of a and expanded our construction to the right.







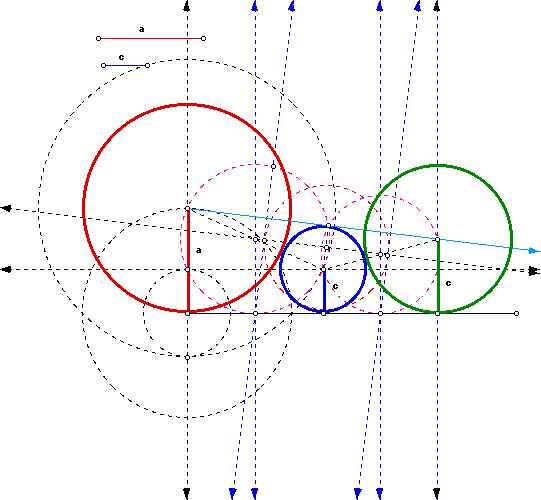
click here for the second GSP construction.

There does exist at least three other construction that demonstrate this particular problem that
have been achieved by our fellow students.









click here to return to home page