The Trisection of a arbitrary triangle. The trisection of a triangle can
be achieved in several ways.
Presented here are four different problems detailing the trisection of an
arbitrary triangle.
The first problem presented here is thus; If a triangle ABC is given and
a random point P
on the one of the sides of the triangle is selected, construct two lines
through P that trisects
the triangle into three regions of equal area.
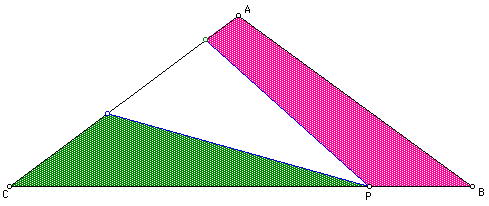
Since P has the ability to be placed anywhere on one of the sides of the
triangle then it is perhaps best to view this as a GSP animation. So click
here for that animation.
The next problem presented is thus; Given a triangle ABC, find a point D
such that line segments AD, BD, and CD trisect the area of the triangle
into three regions with equal areas. Define D and prove that the triangle
is divided into three regions of equal area. Show a construction for finding
D.
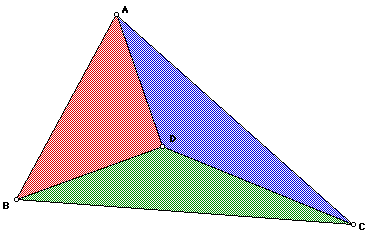
The point D that we see is the intersection of the three medians of triangle
ABC. That intersection point that we call the centriod of a triangle which
is the balance point of the triangle.
click here to see the full construction of point
D.
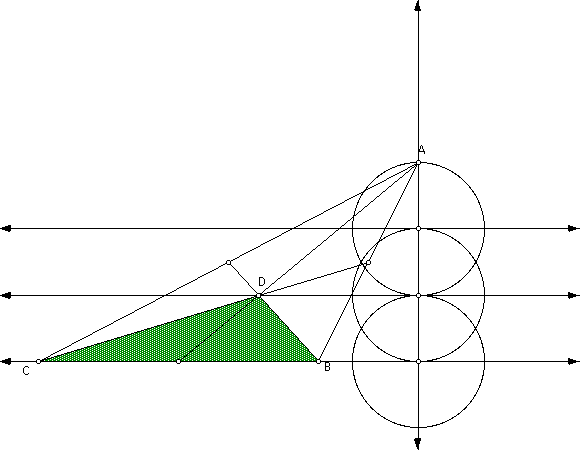
This construction shows the trisection of the altitude from vertex A to
extention of BC. This shows us the altitude of triangle DBC is one-third
that of triangle ABC. Therefore, the area of triangle DBC is one-third
the area of triangle ABC.
click here to return to home page



