EMT assignment 10 piqued my interest in the mathematics of parametric curves.
In that assignment a parametric curve in a plane is defined as "a pair of functions
, x=f(t) and y=g(t), where the two continous functions define ordered pairs (x,y).
The two equations are usually called the parametric equations of a curve. The extent
of the curve will depend on the range of t. In many applications, we think of x
and y varying with time t."
To investigate the problems I chose to use Xfunction as my graphing utility.
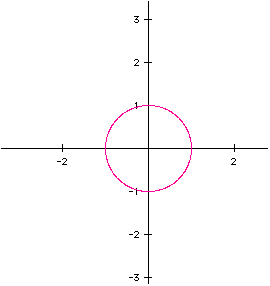
As a starting point I entered x=cos(t) and y=sin(t) for 0<t<6.28. The following
curve results.

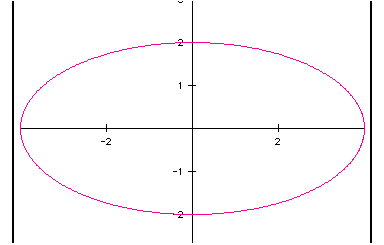
The circle, center at the origin, has a radius of one unit. Knowing the values of cos(t) and sin (t) range from one to negative one, its reasonable the ordered pair (x, y) would do likewise. The pythagorean relationship explains why the curve is a circle. If the equations are modified to include a scalar the radius of the circle changes if the scalar is the same number for both x and y. When the scalars differ for x and y, the curve becomes an ellipse centered at the origin with intercepts of (a,0), (-a,0), (0,b) and (0,-b). This is illustrated for the equations x=4cos(t) and y=2sin(t).
The last step to this exploration will be getting it to come up on my web page...If you're reading it I must have been successful. WOW!