
Department of Mathematics Education
EMT 469

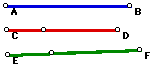
To see a GSP sketch of the completed construction, click here.
An easy way to begin the construction is to construct a triangle that has
the medians for each of its sides. First, construct perpendicular lines.
From the intersection point, copy AB onto one of the perpindicular lines.
From our new point, we strike an arc congruent to CD.Then we can construct
an arc of length congruent to EF so that it and our previous arc intersect.
Connect all intersection points and we have the triangle we desire.
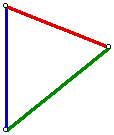
In geometry, there exists a property that states that the medians of
a triangle intersect at a point in which it divides each length of the medians
into a ratio of 2:1. So let us trisect each of the medians we have constructed
above.
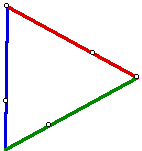
Then construct lines that go through the trisection points:
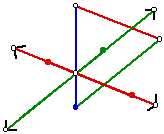
The next step in the construction is to trisect the original medians.
Next, construct a circle with radius 2/3 the original length of the green
median at point P and call its intersection point with the green line point
Q. From point Q, construct a circle with the radius the same length as the
green median and construct a point of intersection W on the green line.
From point P, construct a circle that has a radius of 1/3 the length of
the original red median and call its intersection point with the red line
R. Then from point R, construct a circle with radius the same length as
the original red median and call the intersection point at which it intersects
the red line S. Then draw segments between R and S. Likewise, draw a segment
between W and Q. Now the medians for our triangle have been created.
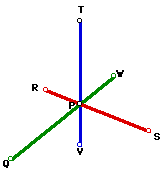
Now construct segments TQ, QS, and ST.
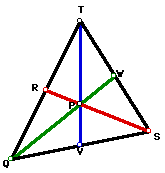
Thus, the construction of a triangle given three medians is complete.
To obtain a GSP script for generating a triangle given its three medians,
click here.
Back to table of contents.