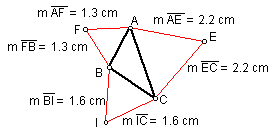
Given triangle ABC, Napolean's triangle is constructed in the following way:
Construct equilateral triangles on each side of the triangle ABC.

Find the centers of each constructed equilateral triangle by finding the angle bisectors of each angle.
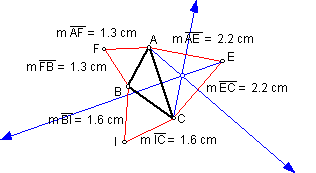
Connect the midpoints of each of the equilateral triangles to form Napoleon's triangle.
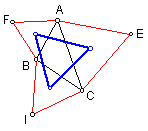
It appears that this newly constructed triangle is equilateral. Animation using GSP confirms this conjecture. If the original triangle is equilateral, then Napoleon's triangle is also equilateral.
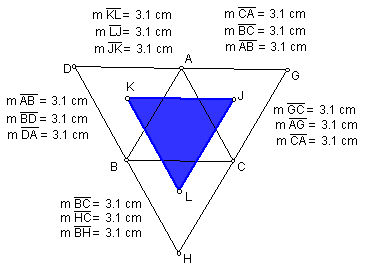
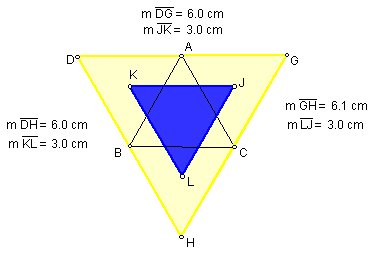
Consequently, the larger triangle formed by the constructed triangles is also equiateral. If Napoleon's triangle is dialated by a scale factor of 2, the larger triangle is formed.
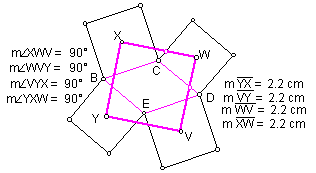
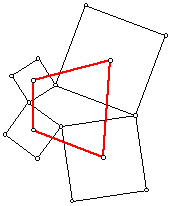
Next, we tried to extend the concept beyond Napoleon's triangle to polygons with more than three sides. The first attempt was with a general quadrilateral. When a general quadrilateral is sketched, and squares are constructed on each side of the quadrilateral there was no apparrent relationship between the figure formed by the centers of the constructed squares.
Next, we investigated special quadrilaterals. When the quadrilateral is a parallelogram, the figure constucted by connecting the centers of the squares constructed on each side of the parallelogram is a square.