
NINE POINT CIRCLE
by Derelle McFarland
Thanks to Euler and Feuerbach we have a way to define and compose a
circle other than by midpoint and radius, by what we call the nine point
circle.
The nine point circle is also called the Euler Circle and the
Feuerbach Circle, because both mathematicians contributed to the circle.
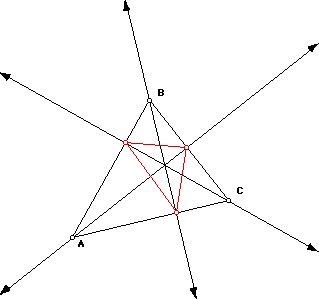
I
will show you how to construct the nine point circle. First given triangle
ABC, construct the altitudes of each side. Then construct a triangle that
connects the points of intersection between the sides of the triangle and
the altitudes.
Then construct the midpoints of each side of the triangle. Then construct
a triangle from these three points.
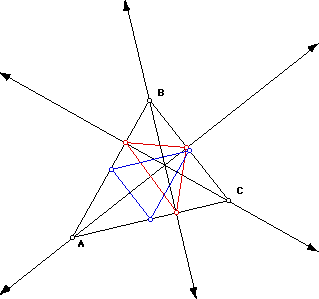
Now construct the orthocenter and construct segments from the orthocenter
to each vertex. Then construct the midpoint of these segments. Then connect
the midpoints to form a third triangle inside the original triangle.

Now we can connect all of the points except for the orthocenter to construct
the nine point circle.
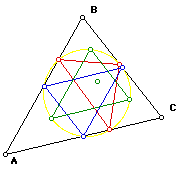
You can construct the nine point circle from any triangle.
The following is the construction of the nine point circle from an equilateral
triangle.
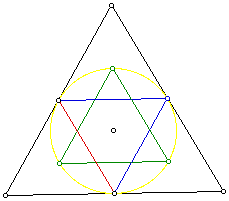
It appears that there are only six point, but in actuality the blue/red
triangle is really two triangles on top of each other. It is obvious that
the blue triangle is the construction of a triangle from the midpoints of
the original triangle, but the red triangle is at the same place because
the altitude of an equilateral triangle goes through the midpoint of the
sides.
An obtuse triangle is a little trickier. The construction of the red triangle
which is the midpoints of the original triangle is simple to construct.
The orthocenter of an obtuse triangle is outside of the triangle. So we
must continue the sides of the triangles so that we can find the intersection
between the altitudes and the sides of the triangle. The constructio will
follow.
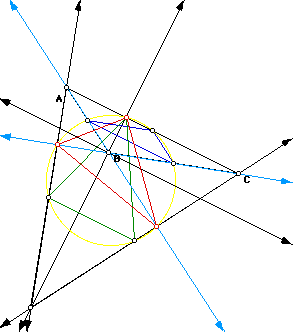
As you see this is a very interesting construction of a circle which
requires students to know other parts of triangles like altitudes and medians.
It could be very useful in a geometry class.
Back to Derelle's Home Page







