---

PEDAL TRIANGLE

by Derelle McFarland

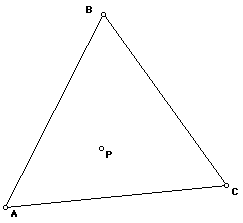
Through the following diagrams I will construct the pedal triangle. I must begin with the antipedal triangle ABC. By definition the antipedal triangle A of a given triangle T is the triangle of which T is the pedal triangle. I'll begin with triangle ABC and pedal point P inside the triangle.

Now, I will construct segments from P perpendicular to sides AB, AC and BC. Then I will construct a triangle from these points.

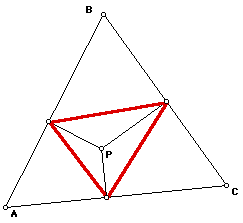
This red triangle is the pedal triangle given point P because the vertices are the feet of the perpendiculars from P to the sides.
I will further investigate the pedal triangle by finding two more pedal triangles to point P by using the previous steps to find the red pedal triangle.

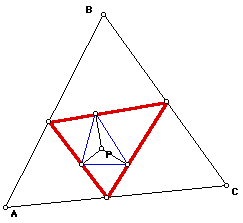
This is the blue pedal triangle. Now I will construct the third pedal triangle, a green one.

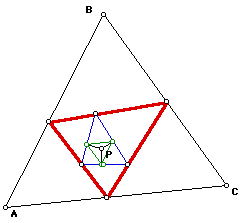
What do we notice from the first pedal triangle (red) and the second one (green)? They are similar. This theorem states that the nth pedal n-gon of any n-gon is similar to the original one.

---

Back to Derelle's home page

---