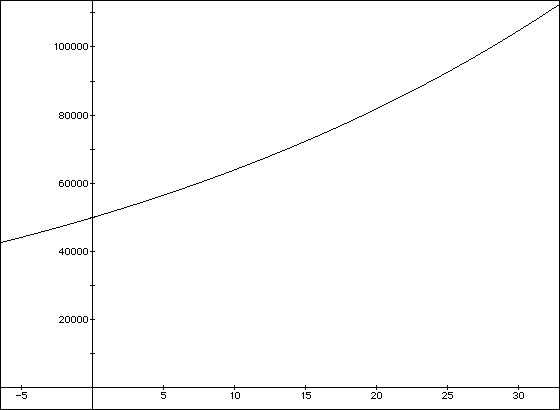Instructional Unit on Exponential Functions

Craig Rimpley

The majority of text books that I looked at cover the topic of exponential functions from a purely algebraic approach. This makes sense since this topic is introduced in an high school algebra II class. Applications are covered in the traditional text, some more than others. What I have attempted to do is create a plan that uses applications to introduce these valuable functions.

GROWTH APPLICATIONS

Mathematics can be used to model certain phenomenon that exist in the real world. We create these models to help us predict the future. One of the functions the mathematicians use is called an exponential function. Exponential functions are of the form: f(x) = A^x , where A is the base and X is the exponent.

The first problem we should look at deals with population growth.

If we look at what makes a population grow over one year maybe we can develop a model that will help us predict the future.

Suppose that the population of a certain town is P is increasing at a constant rate of R each year. We can see that the population of our town one year later will be:

P + P*R = P*( 1 + R )

Two years later the population of our town will be:

P*( 1 + R ) + (P*( 1 + R ))*R = P ( 1 + R ) ^ 2

So, in general the model of population growth looks like:

P*( 1 + R )^ (t-1) + (P*( 1 + R )^ (t-1))*R) = P*( 1 + R ) ^ t , where t is the number of years later.

Now we have a model that we can use to predict the future population of a particular town so the local government will know how to plan for the future growth of the community.

For example, a town has a population of 50,000 that is increasing at a rate of 2.5% each year. Use the model above to predict the population in 10 years.

The first thing we need to do is fill in the correct numbers from our problem into our model.

P = 50,000 people
R = 2.5% or .025
t = 10 years

Our model looks like this:

50,000 * ( 1 + .025 )^ 10 = Y ; add the numbers within ( )

50,000 * (1.025)^ 10 = Y ; use calc. to evaluate (1.025)^ 10

50,000 * ( 1.28 ) = 64,004 ; multiply

So the population of our town will be 64,004 in ten years. What would you do if we needed to know when the population of our town will double? Why don't we use the same approach we used for the first problem. Let's fill in our model!!!

P*( 1 + R )^ t = Y
P = 50,000 people
R = 2.5% or .025
t = ? years
Y = 100,000 people

So our model will look like this:

50,000 * (1.025)^ t = 100,000

Now let's solve for t.

(1.025)^ t = 2

At this time we don't have the algebra skills to solve this exponential function. Could we use our TI-82 to solve for t ?

The answer is YES !!!!!

Enter the equation (1.025)^ t = 2 into the Y= function of your calculator. Now go to the Table function of your calculator and scroll down until the Y1 column reads around 100,000. You can make your answer more accurate by adjusting TblSet on your calculator.

If you would like to see a spreadsheet for this problem CLICK HERE!!!

We can use the graph of this function to check our approximation. We have the function Y=(50000)*(1.025)^ X in our calculator already , so all we need to do is set our window at :

XMIN = -50
XMAX = 50
Xscl = 10
YMIN = -10000
Ymax = 150000
Yscl = 10000

Now use your TRACE function to scroll to where Y is approximately 100,000 and see if X is about 28.

The graph should look like this algebra Expressor file.

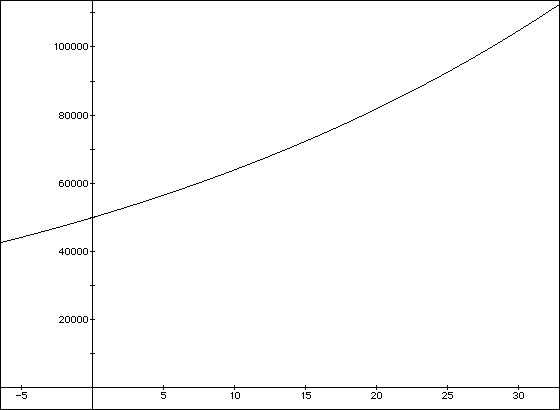
Several types of growth can be modeled using Exponential functions. For example, assume that a certain type of bacterial doubles every hour and there are initially 100 organisms. Lets develop a model for the bacterial growth.

initial amount /////// \\\\\\\one hour later /////// \\\\\\\ two hours later /////// \\\\\\\ three hours later

100 = 100 * ( 1 ) ////////200 = 100 * ( 2 ) ///////////400 = 100 * ( 4 ) /////////////800 = 100 * ( 8 )

100 = 100 * ( 2 )^ 0 ///200 = 100 * ( 2 )^ 1 //////400 = 100 * ( 2 )^ 2 ////////800 = 100 * ( 2 )^ 3

So the model we have developed is Y = 100 * ( 2 )^ X , where Y is the new amount of bacterial and X is the number of hours later.

Let's use this model to solve the following problem. Suppose that the above bacterial will be used in an experiment that allows the bacterial to grow for one day. How many organisms will there be at the end of the experiment if the scientists stared with 100 organisms?

First we need to fill in our model.

Y = ? , this is what we are looking for
X = 24 hours

so our model is Y = 100 * ( 2 )^ 24 ; use your calculator to evaluate ( 2 )^ 24

Y = 100 * (16777216) ; multiply

Y = 1,677,721,600 organisms

Use the TABLE function to check your answer just like we did for the first example.

Here is part of the Excel spreadsheet I used to check my answer.

Number of years later ........................Y=(50000)*(1.025)^ X
.......10 ..........................................................64004.22721
.......11 ..........................................................65604.33289
.......12 ..........................................................67244.44121
.......13 ..........................................................68925.55224
.......14 ..........................................................70648.69105
.......15 ..........................................................72414.90832
.......16 ..........................................................74225.28103
.......17...........................................................76080.91306
.......18 ..........................................................77982.93589
.......19 ..........................................................79932.50928
.......20 ..........................................................81930.82201
.......21 ..........................................................83979.09256
.......22 ..........................................................86078.56988
.......23 ..........................................................88230.53413
.......24 ..........................................................90436.29748
.......25 ..........................................................92697.20492

Now we need to change the problem so we are looking for the amount of time it will take our bacteria to reach a specific amount of organisms.

What if scientist discovered that our bacteria could be used to create a cure for the common cold. The only catch to this remarkable development is that 200,000 organisms are needed to create one dose of the new miracle drug. If the scientist started with 25 organisms, how long would it take for the bacteria to grow enough to make 100 doses of the new medicine?

If we look at the previous problem we can see that we started with 100 organisms. This problem starts with 25 organisms, so our model becomes Y = 25 * ( 2 )^ X . Now all we have to do is fill in our model.

Y = 200,000 * 100 = 20,000,000

So, 20,000,000 = 25 * ( 2 )^ X ; Divide by 25
800,000 = (2 )^ X ; We don't have the algebra needed to solve this problem.

Can we solve for an approximation of X? Yes, use your technology!!!!!!!!

If you would like to see the Algebra Expresser file I used CLICK HERE!!!

If you would like to see the Excel Spreadsheet I used CLICK HERE!!!

FINANCIAL APPLICATIONS

Everyone is interested in money. So let's take some time to look at the some financial applications of exponential functions. Assume that P dollars are invested at a simple interest rate of R, then P is referred to as the Principle and P * R is the amount of interest earned at the end of one period. Now we should be able to develop a model.

If, P + ( P * R ) = principle plus one period of interest

P + 2 ( P * R ) = Total amount after two periods

P + 3 ( P * R ) = Total amount after three periods

P + 4 ( P * R ) = Total amount after four periods

So we can see that the model for X periods of simple interest is:

P + ( P * N * R ) = P ( 1 + N * R ) = Total amount after X periods
OR
P ( 1 + N * R ) = T

So now that we have a model, let's use it to find out how much money we will have in the future!!!

Max deposited $750 in an account that pays 7% simple annual interest. How much money will Max have at the end of five years?

Given our model P ( 1 + N * R ) = T , P = $750 R = .07 N = 5

Simply plug and chug to arrive at the answer.

750 * ( 1 + ( 5 * .07 )) = T ; evaluate on your calculator

1012.5 = T

Wait where is the exponent ? There isn't one, so this isn't an exponential function. Why did we look at this function? Well , most banks don't offer simple interest. What they do is allow interest to compound ; this is to your advantage. When a bank compounds interest they are paying interest on interest.

So we need to create a model for compounding interest. Suppose that we invest P dollars at a rate R compounded 4 times per year, that is called compounding quarterly. We should expect to receive 1/4 of the interest received for one year each quarter. So the simple interest rate in this case where
R = 7% is .07/4.

On the flip side of this we need to see that N becomes the number of times we calculated interest earned. So if we had a problem where interest is compounded quarterly over a 10 year period

N = 4 * 10 = 40

Now our model will take the form:

T = P * ( 1 + ( R/k))^ N

where k = the number of times interest is compounded each year and N = the total number of times interest is compounded.

Let's look at an example.

Max deposited $750 in an account that pays 7% interest compounded quarterly. How much money will Max have at the end of five years?

P = $750
R = .07
k = 4
N = 5 * 4 = 20
So,T = 750 * ( 1 + ( .07 / 4 ))^ 20 ; evaluate on your calculator.
T = $1061.08

Let's investigate other problems concerning compounded interest .

If Drew invested $1550 in a bank that offers a rate of 8.5% compounded quarterly for 7 years and Craig invested $1550 in a different bank at a rate of 8% compounded monthly for 7 years. Who would have more money at the end of 7 years?

This is two problems that we can evaluate using our model and compare.

T1 = 1550 * ( 1 + .085/4 )28 .........................................T2 = 1550 * ( 1 + .08/12 )84

T1 = $2792.73 ................................................................T2 = $2708.50

So, it looks like Drew is the better investor!!!!

Consider the following problem. Craig needs $5000 to buy his uncle's 1967 Corvette Stingray and his uncle has agreed to keep the car until Craig has the money. If Craig has $1200 to invest at a rate of 9% compounded monthly, how long will it take for Craig to get his dream car?

T = $5000
R = .09
k = 12
N = Y * 12, where Y = the number of years
P = $1200
So, 5000 = 1200 * ( 1 + (.09/12))^ (Y * 12) ; divide by 1200
4.1666667 = ( 1.0075 )^ (Y * 12) ; once again we need to go to technology

We should enter the original equation , Y1 = 1200 * ( 1 + (.09/12))Y * 12 , into your calculator and go to the TABLE function or the graph and find the approximation for Y.

CLICK HERE to see the Excel spreadsheet that I used to solve this problem.

This is an Algebra Expressor file I used to check my answer.

Another application to investigate how the total value of an investment changes as the number of times interest is compounded increases. If $1000 is invested at 7% for one year, what is the difference between the total amounts of the investment if the number of times interest is compounded increases.

Compounding ..........................Total value after one year
period

Annually ...............................................T = 1000 ( 1 + .08 ) = $1080.00

Quarterly ..............................................T = 1000 ( 1 + .08/4 )^4 = $1082.43

Monthly ................................................T = 1000 ( 1 + .08/12 )^12 = $1083.00

Weekly .................................................T = 1000 ( 1 + .08/52 )^52 = $1083.22

Daily ....................................................T = 1000 ( 1 + .08/365 )^365 = $1083.28

Hourly .................................................T = 1000 ( 1 + .08/8760 )^8760 = $1083.29

As we can see, this seems to approach some limit as the number of times we compound interest approaches infinity.

When we let the number of times interest is compounded be infinity we say that interest is being compounded continuously. The model that results from this limit is Total = Pe^ RT , where P = the principle , R = the given rate of interest, T = the number of years.

The value of e = 2.718281828........ can be found by evaluating the following summation ;

e = 1 + (1/1!) + (1/2!) + (1/3!) + (1/4!) + ............... + (1/n!).

This is a bit complicated , but can be evaluated by most students with a little guidance.

If you would like to see the Excel spread sheet I used to calculate e CLICK HERE!!!

Lets use our new model for computing the value of an investment when interest is compounded continuously. If Max invests $500 at 7.5% interest compounded continuously, how long will it take for his money to double?

We know the following:

P = $500
R = .075
Total Value = $1000
T = ?

So, our model looks like this :

1000 = 500 e ^ (.075 T) ; divide by 500
2 = e ^ (.075 T) ; go to calculators

Enter Y1 = e ^ (.075 T) into the Y= function and use either your table function or the graph to find an approximation. The answer is somewhere between 9 and 10 years.

If you would like to see the Excel spread sheet In used to solve this problem CLICK HERE!!!

I have successfully avoided the Algebra that is used to introduce exponential functions. The algebra is important but the applications of mathematics is the part that interests most people and I think most students in high school. Obviously the properties of exponential functions need to be seen. As well as logarithmic functions and their properties, so students can gain the ability to solve problems when the technology is not accessible. Wait I can carry my TI-82 everywhere, do think the students have figured this out already?