Parametric equations are one method used to represent curves whose graphs
are not functions. Parametric equations can also be used to look at familiar
functions. In this investigation, we will examine lines defined by parametric
equations and comment on how the parameter, t, determines the values of
x and y and hence, the extent of the curve. Consider parametric equations
of the form
As we examine parametric equations of this form for different values
of a, b and k, we will look at how this change affects not only the extent
of the curve, but also, the graph of the line.
Consider the parametric equation
In this example, we have a = 6, b =1 and k = 1. Graphing the equation
below we obtain
.
In this example, the range for the parameter t has been defined as -10 t
10. If we examine the range of values for x, we find the graph extends from
-4 x 16 which is what we would expect as we substitute in the full range
of t values. Similarly, we find the range of values for y with -9 y 11.
In fact, the general form of the equation under consideration will have
for -L t L a range of
Now consider the nature of the line itself. Here, we can observe the
y-intercept is -5 with slope 1. What is the relationship between a, b, and
k in the general parametric equation we are considering and the nature of
the line, that is, the slope and the y-intercept ? In this example, we obtain
the y-intercept by subtracting a and b but the slope of the line is not
immediately obvious.
If we change the value of k to 3 and -3, we obtain the following graphs.
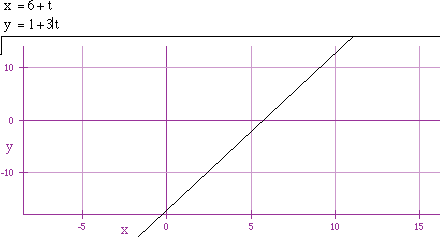
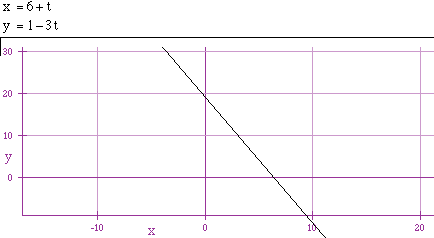
In the above graphs, we observe that k changes not only the slope but also
the y-intercept. Again looking at the general form of the equations,
we can solve each equation for t and set the two equations equal to obtain
For the two examples given above, we can obtain the slope as k and the
y-intercept as -ka+b. Thus for the second example, we have a slope of -3
and a y-intercept of 19.
With this information not only are we able to find the slope and y-intercept
of lines written in parametric form, we can also use this to find the parametric
equations of lines given the slope and y-intercept.
Next, consider how to construct a line in parametric form given a point
and the slope. Taking
and putting this in point slope form, we obtain
Writing the equation in this form gives us the relationship we are looking
for, that is, a, b, and k in the general form of the parametric equations
we are considering are slope, k, and a point on the line (a,b).
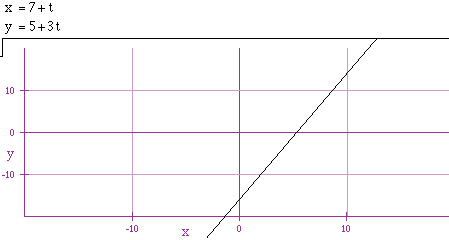
Thus, if we consider a line passing through (7,5) with slope 3 (problem
#7 on assignment 10), we are able to write the parametric equations for
this line as
Graphing the parametric equations we obtain the following sketch.
