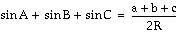sin A + sin B + sin C in a triangle.

HINT 2

Consider the triangle and its circumcircle. Draw diameter of the circumcircle from B to A'.

Now, the angles at A and A' have the same measure. The sin A = sin A'.

But

sin A = sin A' = a/2R

Where R is the radius of the circumcircle. So,

Return