VECTORS
An Essay
Written for: Dr. J. Wilson
Ma 669, Winter Quarter
Written by: Sandra M. McAdams
The essay includes an historical perspective,vector descriptions and operations and vector applications.
Historical Development of Vector Analysis
The following essay will discuss the history in the development of vector quantities and the analysis of vectors, possible activities to use in classroon instruction and applications of vector analysis that could be used in a lab or classroom setting. Vector analysis used today is directly related to William Rowan Hamilton's work done on quarternions. Hamilton, an Irishman, was a child prodigy in the field of languages having mastered eleven languages in as many years. At the age of fifteen he became interested in mathematics after meeting an American ,Zerah Colburn ,at an exhibition in Dublin. With his new found interest Hamilton read and mastered analytic geometry and calculus, and after reading the great mathematical works of the continent he uncovered a mathematical error in Laplace's Mecanique Celeste which drew considerable attention. The following year he entered Trinity College in Dublin, and as a twenty-one year old undergraduate he was elected unanimously as the Royal Astronomer of Ireland, Director of the Dunsink Observatory, and Professor of Astronomy at the University. After many significant contributions and several years of service at the University he devoted much of his time to developing quaternions which he felt would be of revolutionary significance in mathematical physics. In the early nineteenth century who could believe that there could exist an algebra different from the common algebra of arithmetic. Hamilton was forced by physical considerations to investigate an algebra for which the commutative property of multiplication did not hold. Hamilton had already found a convenient way to study vectors and rotations in the plane by developing an algebra that converted the complex numbers into real number ordered pairs. He wanted to develop an analygous system of numbers for the study of vectors and rotations in three-dimensional space. He was led to consider ordered real number quadruples (a,b,c,d) having both the real and the complex numbers embedded within them. He called such real numbered quadruples quaternions. He found for his various purposes he needed to formulate definitions for addition and multiplication of these numbers. While addition did not pose a problem, he found that the commutative law for multiplication would not suffice. After literally studying this multiplication for years he found that it came to him instantaneously while walking with his wife one evening. He was so struck by this idea that he literally carved the gist of it into one of the stones on Broughm Bridge. Today a tablet embedded in the stone of the bridge reveals the story. His Treatise on Quaternions appeared in 1853 when he was 48 years old. Unfortunately for Hamilton he did not complete his next treatise. He died in 1865 essentially from alcholism. Although his personal life seemed to be unhappy, his professional life was filled with honors and appointments of great standing. The quaternions over time became a disappointment. Hamilton thought that they would become the mathematical language of physics, however they were relegated to simply an interesting work in the history of mathematics due in part to an American mathematician, Josiah Gibbs of Yale University. Using a departure from the quaternion representations found by Hamilton, Gibbs built a system of three dimensional vector analysis. He used just the vector portion v = bi + cj + dk to represent physical quantities. In the place of Hamilton's single quaternion product which Hamilton worked on for years, Gibbs introduced two different types of multiplication: the scalar or dot product and the vector or cross product.
The scalar or dot product for three dimensional vectors was defined as follows:
Let v = bi + cj + dk and Let v' = b'i + c'j + d'k, then v dot v ' = bb' + cc' + dd'
The vector or cross product for three dimensional vectors was defined as:
v X v' = (cd' - c'd) i + (db' - b'd)j + (bc' - b'c)k
The vector analysis of Gibbs eventually replaced the more complicated quaternions for the practical purposes of physics and engineering. Although quaternions failed to be the useful tool that Hamilton had hoped his great labor in bringing forth this concept was not wasted. The key step in abandoning the commutativity law was instrumental in the development of modern algebra. They showed that it is possible to consciously construct new elements of algebra which opened up new possiblities for those who followed.
Vectors - Descriptions and Operations
A vector quantity is a quantity that has both magnitude ( length) and direction. A force is an example of a vector quantity because to describe it you must tell the direction in which it is acting and the strength applied. Velocity is another example of a vector quantity as its description includes direction and speed. A scalar quantity has no direction. For example speed is a scalar quantity. Volume, length and weight are also scalar quantities. For a specfic example of a vector quantity consider a plane flying due north at 550 knots. Its vector could be represented by an arrow 550 units long pointing at a bearing of due north which is represented in polar form as 90 degrees.

This velocity ( 550 knots) is called a velocity vector and may be denoted by the symbol v. To say that two vectors are equal does not mean that they are identical however. Vector v is equivalent to vector u if v and u are the same length and have the same direction. One may be a translation of the other.
Definitions:
A Vector is a directed line segment.
Two vectors are equal if and only if they have the same magnitude and direction.
The absolute value of a vector is its length or magnitude and is found by the Pythagorean Theorem.
There are various operations that can be done with vector quantities. We will discuss vector addition, find the absolute value or magnitude of a vector, find the scalar product and dot product of two vectors, and do various applications with vectors.
Addition of vectors: Two Approaches
Adding Vectors Geometrically
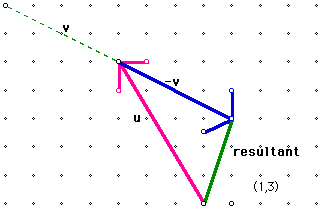
Consider again the velocity vector v of the airplane flying due north at 550 knots. Assume it encounters a wind w blowing toward the southeast at 100 knots. The resulting velocity of the plane is represented in the diagram below. This resulting vector is called the resultant. The resultant r is actually representing a vector sum i.e. r = v + w . In order to add two vectors geometrically we place the head of the second vector at the tail of the first then draw a resultant vector from the tail of the first vector to the head of the second or last vector. This can be generalized for several vectors. See picture below where two vectors are added geometrically. Note the position of the two vectors.

Adding vectors algebraically
Algebraically vectors can be represented as ordered pairs of numbers. This can be done in two ways, in polar form or component form. The component form allows us to view the vector as a displacement and therefore add them easily. In general if the vector v is represented by (a,b) this indicates that the vector consists of "a "units in the x -direction and "b "units in the y -direction. The numbers a and b that appear as ordered pairs are called the x and y components or simply components. It is very simple to add vectors in component form since we can add the x components and the y components to yield the components of the resultant vector. Using the example from earlier with vectors v and w, v would have components (0,550) while w would have components at approximately (70.71, -70.71). To add these component wise would give a resultant of (70.71, 479.29) In polar form the vectors would be (550, 90 degrees) + (100, 315 degrees). In order to add these component wise when given polar form return to the definition of polar form
(x,y) = (rcos ø, r sinø). This would yield (500 cos 90+ 100 cos 315, 500 sin 90 + 100 sin 315) = ( 70.71, 479.29). To find the length of the resultant use the absolute value of the vector i.e. apply the Pythagorean Theorem to the two legs ( the horizontal and vertical components) given and this will give the magnitude of the resultant.
The absolute value or magnitude of ( v + w) = 484.47. In the drawing above the magnitude of the resultant is approximately 480 units.
Opposite Vectors ,Scalar Multiples, Vector Subtraction, Zero Vector
Recall vector v and vector u are defined to be equal when they have the same magnitude and direction. The opposite of a vector is a vector which has the same length but it is opposite in direction, i.e. it is 180 degrees from the original given direction. An example follows:
Let u =( 3, 4) find -u.
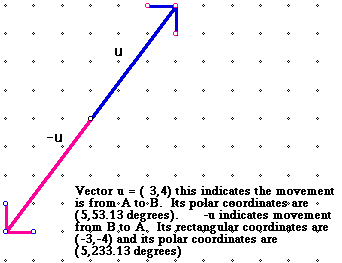
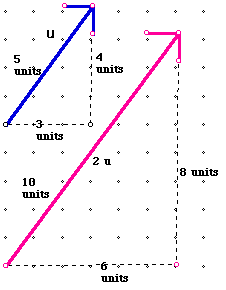
Note the rectangular coordinates of -u are ( -3,-4). This is essentially multiplication by the scalar negative one. A scalar is simply a real number. We refer to scalars when doing operations with vectors to differentiate the two types of quantities. If we multiply a vector by a scalar k we obtain another vector k times as long as the original. To find an opposite vector we can multiply by negative one; we are not, however limited to multiplication by -1. We can multiply a vector by any real number k and obtain a new vector with the same direction as the original and each (x,y) pair becomes (kx,ky) . Using the same vector u, given in the first example find 2u. You can check your diagram to be certain that the length is twice as long by using the Pythagorean Theorem.
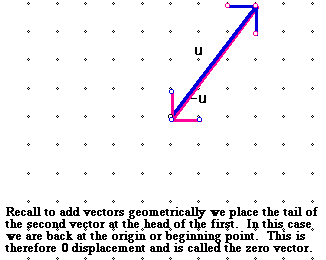
It is also worth noting at this point that there is a zero vector. We may think of a zero vector as a point. The displacement of the object is zero and its initial and final positions are the same. If we add u to -u we obtain the zero vector.
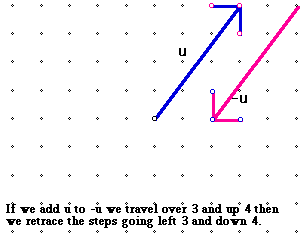
To subtract these two vectors recall we will place the tail of the second vector at the head of the first. ( See below) In subtracting u - u we obtain the zero vector.
We may, of course subtract vectors that are not opposite vectors. For example:
let u = ( -3,5) and v = ( -4, 2), find u - v.
Component wise subtraction yields the rectangular coordinates (1, 3). Subtracting geometrically means adding the opposite of v to vector u.
Dot Product
Recall in the introductory remarks, historically Hamilton contemplated vector multiplication for several years and it was not until he was able to throw out the commutative property for multiplication that he was able to satisfy this operation. There are two types of multiplications defined for vectors. Let u = (a,b ) and v = (c,d) then the dot product of these two vectors is defined as ac + bd. This of course yields a scalar not a vector. It is interesting to note that if and only if the dot product is equal to zero then the vector u and v are perpendicular to one another. Also u is parallel to v if and only if u = k v where k is a scalar and u and v are not equal to the zero vector. For example : Show that if u = (3, -6) and v = ( 4,2) then u is perpendicular to v.
u dot v = (3)(4) + (-6)(2) = 0; Since the dot product is zero the vectors are perpendicular or orthogonal to one another.
The cross product allows for a nice introduction into vectors and matrices and three dimensional vectors.
The following are a few application problems that students might find interesting. It is suggested that a diagram always accompany any solution. Some of these problems are taken from Precalculus with Trigonometry by Foerster others are from Flying Through Vectors.
I. Shot on goal.
Two soccer players kick the ball at the same time. One player's foot exerts a force of 70 Newtons west while the other player's foot exerts a force of 50 Newtons north. Assuming the players are reasonably close to the goal and the goal is at a bearing of 306 degrees from their location, will this be considered a shot on goal? Draw a diagram. Use bearing angles.
II. Extracting Force
Two archeologists discover something large at an excavation site. Believing it may be a dinosaur bone Dr. Raptor and Archie Optimist attach ropes to their buried treasure and approximate that they need 300 pounds of force to do the job. If Dr. Raptor pulls at a force of 150 pounds, and his assistant pulls with a force of 250 pounds at what angle must they pull in order to exert exactly 300 pounds of pressure?
III. Hot Air Balloons
Balloons are completely dependent upon the prevailing winds so the speed of a balloon is the same as the speed of the wind. Usually the wind direction and wind speed change with altitude. The lower you are the less wind there is. Note also that a balloon flies the opposite of the wind direction. For example if the wind is coming from the west the balloon will fly due east. Consider this when studying the following diagrams. Also realize that bearing angles are used in this problem. The following are some typical examples of wind direction and speeds to use with the problem.


1.A balloon takes off from a soccer field. The vertical speed is 2700 meters per hour. At which altitude will the balloon pass the trees as indicated in the illustration below?

2. A balloon start at Albuquerque. It flies as follows:
the first half hour at 300 meters
then an hour at 900 meters
finally, a half an hour at 300 meters, Draw the route.
The following are some simple applications for vector addition. It is important for the student to understand conceptually what is going on. To assure understanding it is important for diagrams to be drawn. Many students will want to use the calculator for all computation without doing the drawings. I do not recommend this. Even though the graphing calculators will convert from rectangular to polar coordinates and readily compute the resultant in rectangular form, students who approach problems in this way will often have no conceptual understanding to solve problems on their own. Additionally they will not realize that they are getting answers in the wrong quadrants based on principle values found in their calculator.
Vector Practice
Draw diagrams to fit each of the following problems. Note whether the problem involves bearing.
1.Given vector v with a magnitude of 5 and direction of 70 degrees and u with a magnitude of 6 and direction of 25 degrees find the resultant r.
2. A ship sails for 20 miles on a bearing of 325 degrees and then turns and sails on a bearing of 250 degrees for 7 more miles. Find the displacement vector d, from the starting point.
3.A plane flies 200 mph along a bearing of 320 degrees. The air is moving with a wind speed of 60 mph along a bearing of 190 degrees. find the plane's resultant velocity ( speed and bearing) by adding these two velocity vectors.
4. Portia Udell walks on a bearing of 90 degrees for 100 meters and then on a bearing of 180 degrees for 182 meters. What is her bearing from the starting point?
5.Joe Jamoke and Ivan Hoe are pulling up a tree stump. Joe can pull with a force of 200 pounds and Ivan with a force of 250 pounds. A total force of 400 pounds is sufficient to pull up the stump. If they pull at an angle of 25 degrees to each other will the sum of their force vectors be enough to pull up the stump? ( This problem will require the law of cosines.)
6. The world has been attacked by hostile aliens. This is a job for Superman! He wants to rid the world of these dangerous aliens forever. As they fly away, they must pass close to the sun. They are on a heading of 90 degrees with a speed of Warp 8. If Superman can change their course to a bearing of 60 to 64 degrees, they will crash into the sun. If he gives them a velocity of Warp 4 and a bearing of 0 degrees, has good triumphed?