
Square Ratios
This problem was actually found under the papers section on the web but we found it to be interesting and therefore began an exploration with it before reading the entire paper.
The Problem:
Given a square of side s and segments drawn from each vertex to the midpoint of the second side, counting counter-clockwise. The segments intersect to form a new square. What is the ratio of the area of the shaded square to the area of the original square?

Preliminary Attempts and Findings:
In exploring this problem we first solved it on paper by letting the sides of the large square be equal to 2 units. By using trigonometry we were able to find the following measures which we transferred to GSP.
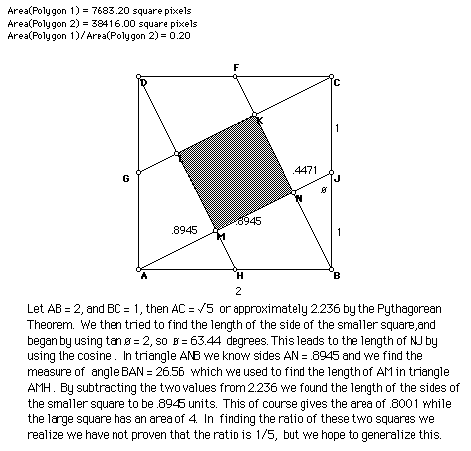
Algebraic Proof:
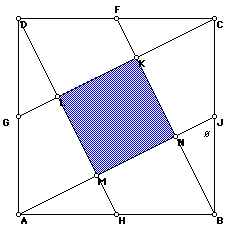
Given square ABCD with side midpoints F, G, H, and J.
Let AB = 2a. Then JB = a, since J is a midpoint.

Next we will find the measure of MN to compare areas. First,
![]()
Using the Arcsin function, therefore A = 26.565 degrees and J = 63.435 degrees
We are given square KLMN, therefore AMH = 90 degrees since LMN and AMH are vertical angles.
Using the subtraction postulate AHM = 63.435 degrees and MAH = 26.565 degrees
Using similar reasoning the measures in triangle NJB can be found. Once we know these angle measures we can find the lengths of AM, MN, and NJ.
Sin 26.565 = NJ/ a and so NJ = .4472a
Sin 63.73 = AM/a and so AM = .8967a
Now, by subtraction, MN = .8944 a.
We have:
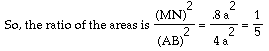
Applications to the Secondary Classroom:
This problem is a good exercise in trigonometry concepts and would make a nice lead in into algebraic proof. Most students in the Integrated 3 curriculum ( 10th grade honors) would be able to do the trigonometry required and could reason through a narrative proof of this type. This is a concrete example of how we might reason through a problem by assigning values and then go back through with variables to prove the general case.