
The same volume can be expressed in several ways. To make a guess as
to the volume, it may be easier to guess in cups rather than centimeters
or inches. One may visualize that a 12 ounce soda can is about 1.5 cups.
This is equivalent to 354.88 cubic centimeters or 21.656 cubic inches.
A calulator such as the TI-85 may be used to find these conversions. One
can simply type in the number of ounces, tell the calculator what unit of
measurement to convert to, and it will do it for him or her.
I measured a soda can in order to compute an estimate of this volume. I
measured 8.1875 inches for the circumference, and 4.75 inches for the height.
Using the formula for a right circular cylinder, I estimated that the volume
was about 25.219 cubic inches. This estimate is "off" because
of measuring error and because soda cans are not exactly right circular
cylinders.


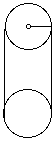
The above left picture shows a right circular cylinder. (The picture
on the right shows a side view of a right cylinder.)
When I measured the height of the can, I measued from the top of the can
to the bottom of the can. However, the 12 ounces of liquid that are in the
can do not go to the very top of the can. One could try to compensate for
this by attempting to measure from the bottom of the can to the top of the
liquid. But if I still use the right circular cylinder formula, my estimate
will again be too high since I haven't accounted for the tapered shape that
the bottom (and top) of a soda can has.

The above picture shows a side view of a soda can. The shaded region
denotes the liquid inside the can. Notice the difference in this shape as
opposed to the side view of a right circular cylinder.
One obvious extension of this problem would be to find the volume of different
sized cans. One could also try to estimate volumes of different shaped containers.
Several factors are considered when a product is marketed. For example,
manufacturers want soda cans to be visually appealing to customers, and
they want each can to fit nicely in an average sized hand. They may also
want to minimize cost by minimizing the material needed to make a can of
a given volume. This can be done by minimizing surface area.
In a previous EMT 669 essay, I looked at ways to find the minimum surface
area of a right circular cylinder. Click here
for that essay. (Use the Back key to return here.)