Maximum Rectangle Inscribed in a Triangle

Lori Pearman
EMT 725

Problem: Find the maximum rectangle inscribed in a triangle.

Given a triangle, how could one construct the inscribed rectangle with maximum area?
I began this investigation by randomly drawing a triangle in GSP, inscribing a rectangle in it, and animating a point in such a way as to show all possible inscribed rectangles. I then calculated the area of the rectangle in order to look (as the rectangle was animated) for the maximum area. For the triangles that I tried, the maximum rectangle occured when the midpoints of two of the sides were joined to make a side of the rectangle. Click here to see an example.
If my conjecture was true, then to constuct the inscribed rectagle of maximum area for a given triangle, one shoud do the following: find the midpoints of two of the sides of the triangle, and join these midpoints to make one side of the rectangle. Dropping perpendiculars from the midpoints will determine the lengths of the other sides of the rectagle. ( The intersection of the perpendiculars and the 3rd side will be the other two vertices, besides the midpoint vertices.) Click here to see a script that will contruct this rectangle given the vertices A, B, C of some triangle.

The above picture gives an example of a triangle whose inscribed rectangle of maximum area has been constucted. Notice that the area of the rectangle is half the area of the entire triangle. This will be the case for any inscribed rectangle of maximum area.

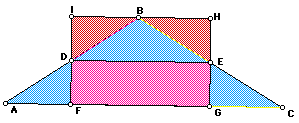
The above picture will help to demonstate why the inscribed rectangle of maximum area (the pink rectagle in this picture) has an area which is half that of the big triangle. To make this picture, I rotated triangle ADF 180 degrees about the point D to create triangle IDB. Similarly, triangle BHE was created by rotating triangle EGC about point E. If we were to delete triangles ADF and EGC, then what we would have left is two rectangles DIHE and FDEG which have the same area. Thus, rectangle FDEG is 1/2 the big rectagle FIHG. Since the big rectangle is equal in area to the big triangle that we started with (because we simply rotated two parts of it to make the big rectangle), rectangle FDEG = (triangle ABC)/2.

How do you know that rectangles DIHE and DFGE have equal area without using GSP to measure their areas? Let's look at the side where triangle ADF was rotated to make DIB. (A similar argument can be made for the other side with triangle BHE.) DIHE and DFGE have equal widths. ID = DF since DF was rotated to make ID. Both of these rectangles have a length that is equal to DE. Also angle AFD was right, so angle DIB is right. AD = DB since D is the midpoint of AB. When triangle ADF is rotated, AD "fits" exactly on DB.