Lori Pearman
EMT 725
Problem: A Bronco was originally fitted with 30 inch tires. Thus,
the speedometer is calibrated for 30 inch diameter tires. 31 diamter tires
were then put on the Bronco. How did this change the speedometer readings?
What should the driver make the speedometer read (with the 31 inch tires)
so that the actual speed is 55 mph?
Solution: Let's compare the "smaller tire truck" with the
"big tire truck". Let D1 be the distance traveled by the smaller
tire truck and D2 be the distance traveled by the big truck. Also let d1=
30
= smaller diameter, and d2 =31 = bigger diameter.
Assume D1 = D2. Let's change these distances to revolutions:
D1 [1 revolution/((pi)d1)] = D2 [ n revolutions/((pi)d2)]
1/d1 = n/d2 implies n = d2/d1
Now let t1 = revolutions of the smaller tires and t2 = revolutions of the
bigger tires. Then t1 = n (t2) for the same distance traveled.
For the smaller tires, C (t1) = speedometer reading, where C is some constant
(determined by tire size and axil gears) that gives a mph reading when multiplied
by the # of tire revolutions (t1 in this case). So we're interested in C
(t1) = 55. This implies that t1 = 55/C.
For the bigger tires, we have C (t2) = x, where x is the speedometer reading.
Because t2 = t1/n = (t1)(d1/d2), plugging in for t2 gives: C ( t1 (d1/d2))
= x.
So... C [(55/C)(d1/d2)] = x.
55 (d1/d2) = x implies 55 (0.9677) = x.
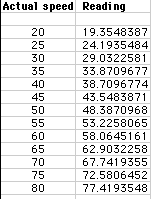
The speedometer reading for an actual speed of 55 mph is x = 53.2258.
We could use the equation s (d1/d2) = x to get several speedometer readings
for actual speeds s.
Return to Lori's EMT 725 Page

