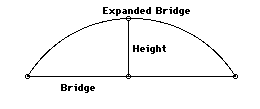

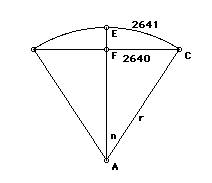
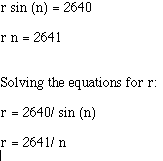
The solution to this system is not obvious. We created a spreadsheet
to substitute a value for n, evaluate the value of sin (n), and compute
the value of r in each equation. Then the spreadsheet calculated the difference
in the values of r for each equation. When we found a value for n which
created a value for r in each equation with differences close to zero, we
continued to add significant digits to our n value in order to get closer
to a zero difference.
After deciding that the value of n =.04766, we calculated the radius from
the above equations and found r =55406.369. Then we had to calculate x in
the picture below:
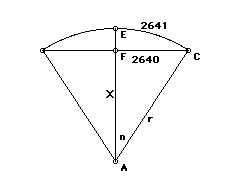
This value was calculated using the value of r and the pythagorean theorem
and found to equal 55343.43796. After subtracting r, the bridge is found
to rise vertically 62.93 feet.
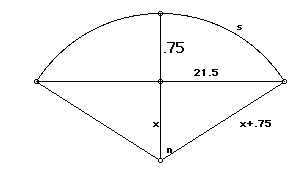
We used the pythagorean theorem and solved for x=307.79166 feet. This
means r= 308.5166 feet and n=.069739163. Therefore s=21.51568 and the entire
bridge length is approximately 43.0313 feet.