EMT668
Write-Up 3
Prepare a summary and explanation of the following investigation.
A. Take any triangle ABC. Construct equilateral triangles externally
on each side and locate the centroid of eaCh equilateral trainagle. Label
these centroids A', B', and C' for the triangle centroids opposite angles
A, B, and C.
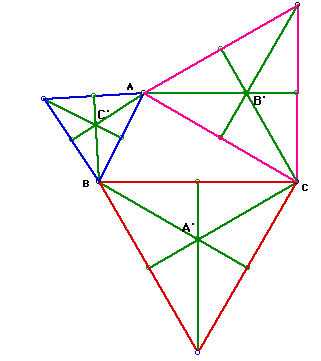
Construct lines AA', BB', and CC'. Observe. Are they concurrent?
Is the point of concurrency any of the orthocenter, centroid, incenter,
or circumcenter of triangle ABC? If not, what can you find out about this
point?
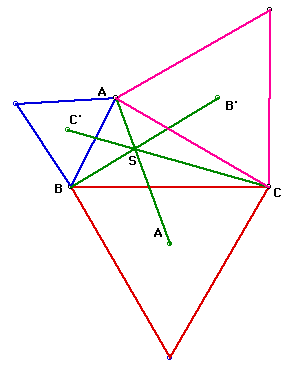
I chose to label the point of concurrency, S. The question becomes, is
S the point of concurreny for the lines of the orthocenter, centroid, incenter,
or circumcenter of the triangle ABC?
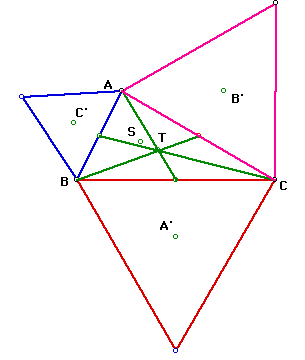
The point T is the centroid of triangle ABC. As you can see T and
S are not the same point.
For the sake of space I will show the points of concurrency for the orthocenter,
circumcenter, and incenter for triangle ABC on one picture.
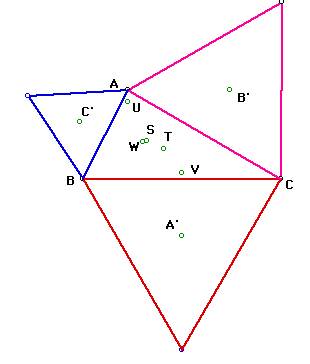
In the above picture U is the orthocenter, V is the circumcenter, and
V is the incenter of triangle ABC. As the picture demonstrates none of the
centers of triangle ABC is the same as point S.
In trying to determine a relationship between S and the triangle ABC,
I first constructed the segments that connected the vertices of traingle
ABC with S. I then tried to determine if I could find a relationship between
those segments.
This is a picture representation of that effort.
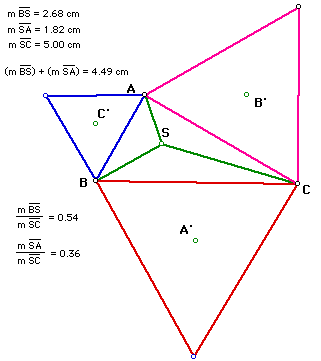
As you can see, I tried determining if there was a common ratio between
the segments and I also thought that the length of the longer segment might
be equal to the sum of the lenghts of the shorter segments. Neither of
those conjectures were true.
I then decided to take a different approach. What if I constructed
a triangle within triangle ABC that had its vertices at the midpoint of
the segments in triangle ABC? Following is a picture of that representation
and an explanation of what I tried in an effort to determine the relationship
S has with triangle ABC.
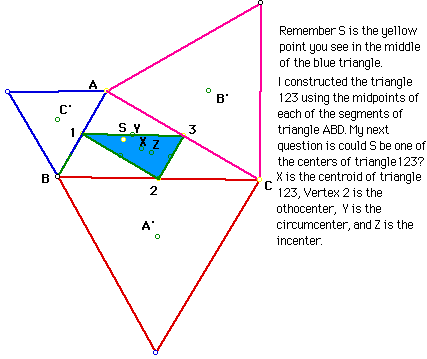
Thus far I have not been very successful in determing the relationship
that S has to triangle ABC. I am sure that eventually I will ask the right
question of myself and find the answer to the problem.
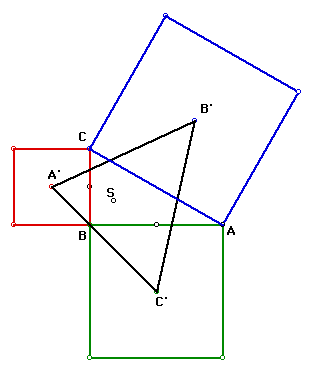
Next, I will do the same investigation using squares instead of equilateral
triangles. The centers of the squares will be A', B', C'.
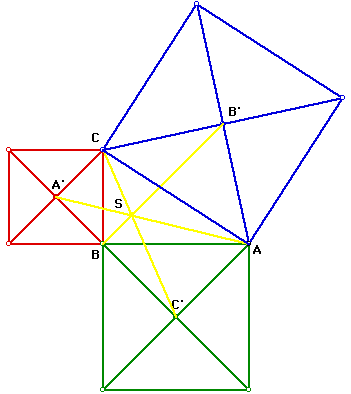
In the above picture S represents the point of concurrency of segments
AA', BB', and CC'. I will now try to determine if any of the centers of
the triangle ABC are at point S.
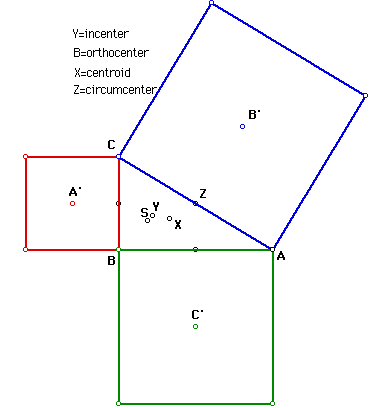
The above picture gives you an idea about where to start furhter
investigations into the centers of triangles and their relationships to
other geometrcic figures extended from the sides of the triangle. I thought
that it would be interesting to explore the triangle A'B'C'. What does
that triangle have in common with the triangle ABC.
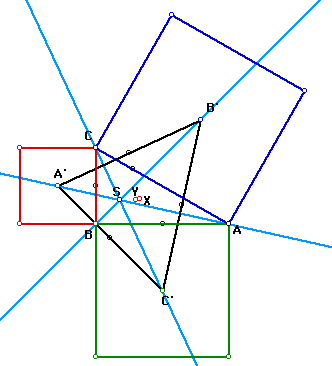
Below is a picture of the construction of the orthocenter of triangle
A'B'C'. As you can see I finally found a center that was shared between
different triangles!!! Of course this is NOT a proof that the orthocenter
of triangle A'B'C' is always have the same point of concurrency as AA',
BB', CC'.
The discussion of the centers of triangles can go on forever. There
is no limit to the types of things we can try now that technology has made
it so easy to quickly make geometric contructions.
Return to T.Wright's problem
page










