

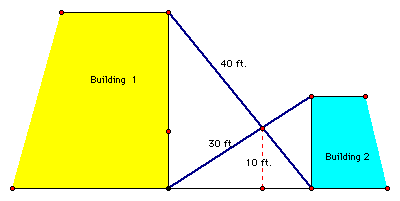
Two buildings are separated by an alley. Two ladders are placed so that the base of each ladder is against one of the buildings and reaches the top of the other building. The two ladders are 40 feet and 30 feet long. Further, they cross at a point 10 feet from the ground. How wide is the alley?
Compare this problem with Distance Survey.
Hint: See Segment Parallel to Bases of a Trapezoid through Intersection of Diagonals. The ladders represent the diagonals of a trapezoid.
Is this a consistent construction? Can you in fact have lengths of 40 and 30 as the diagonals of a trapezoid with two right angles such that the diagonals cross at this a distance of 10 from the side perpendicular to the two bases? Demonstrate the construction or provide evidence that it can not be done.